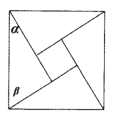
【题目】《周髀算经》中给出了弦图，所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形，若图中直角三角形两锐角分别为
，
，且小正方形与大正方形面积之比为
，则
的值为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
设大的正方形的边长为1，由已知可求小正方形的边长，可求cosα﹣sinα=
，sinβ﹣cosβ=，且cosα=sinβ，sinα=cosβ，进而利用两角差的余弦函数公式，同角三角函数基本关系式即可计算得解．
设大的正方形的边长为1，由于小正方形与大正方形面积之比为9：25，
可得：小正方形的边长为，
可得：cosα﹣sinα=，①sinβ﹣cosβ=，②
由图可得：cosα=sinβ，sinα=cosβ，
①×②可得：
=cosαsinβ+sinαcosβ﹣cosαcosβ﹣sinαsinβ=sin2β+cos2β﹣cos（α﹣β）=1﹣cos（α﹣β），
解得：cos（α﹣β）=
．
故选：D．
科目：高中数学 来源： 题型：
【题目】已知函数
的定义域为
，部分对应值如下表．
x |
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
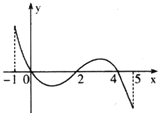
的导函数
的图象如图所示：下列关于的命题：
函数是周期函数；
函数在
是减函数；
如果当
时，的最大值是2，那么t的最大值为4；
函数
的零点个数可能为0、1、2、3、4个．
其中正确命题的序号是______．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆
．
（1）若椭圆
，判断
与
是否相似？如果相似，求出与的相似比；如果不相似，请说明理由；
（2）写出与椭圆相似且焦点在
轴上、短半轴长为
的椭圆
的标准方程；若在椭圆上存在两点
、
关于直线
对称，求实数的取值范围；
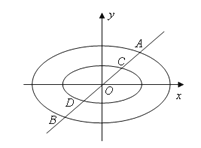
（3）如图：直线
与两个“相似椭圆”
和
分别交于点
和点
，试在椭圆和椭圆
上分别作出点
和点
（非椭圆顶点），使
和
组成以
为相似比的两个相似三角形，写出具体作法．（不必证明）
查看答案和解析>>
科目：高中数学 来源： 题型：
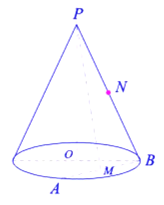
【题目】已知圆锥的顶点为
，底面圆心为
，母线长为
，
，
、
是底面半径，且：
，
为线段
的中点，
为线段
的中点，如图所示：
（1）求圆锥的表面积；
（2）求异面直线
和所成的角的大小，并求
、两点在圆锥侧面上的最短距离.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
过点
，且与
轴、
轴都交于正半轴，当直线与坐标轴围成的三角形面积取得最小值时，求：
（1）直线的方程；
（2）直线l关于直线m:y=2x-1对称的直线方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的首项
， 
， 
．
(1)求证：数列
为等比数列；
(2)记
，若Sn<100，求最大正整数n；
(3)是否存在互不相等的正整数m，s，n，使m，s，n成等差数列，且am－1，as－1，an－1成等比数列？如果存在，请给以证明；如果不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB＝1，BC＝2，CD＝1＋
，过A作AE⊥CD，垂足为E，现将△ADE沿AE折叠，使得DE⊥EC.
(1)求证：BC⊥面CDE;
(2)在线段AE上是否存在一点R，使得面BDR⊥面DCB，若存在，求出点R的位置；若不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
