
【题目】已知圆锥的顶点为![]() ,底面圆心为
,底面圆心为![]() ,母线长为
,母线长为![]() ,
,![]() ,
,![]() 、
、![]() 是底面半径,且:
是底面半径,且:![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 的中点,如图所示:
的中点,如图所示:
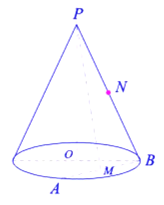
(1)求圆锥的表面积;
(2)求异面直线![]() 和
和![]() 所成的角的大小,并求
所成的角的大小,并求![]() 、
、![]() 两点在圆锥侧面上的最短距离.
两点在圆锥侧面上的最短距离.
【答案】(1)![]() ;(2)
;(2)![]() 、
、![]() 夹角为
夹角为![]() ,最短距离为
,最短距离为![]()
【解析】
(1)由![]() 求得底面圆半径,根据圆锥表面积公式可求得结果;
求得底面圆半径,根据圆锥表面积公式可求得结果;
(2)作![]() ,根据异面直线所成角定义可知所成角为
,根据异面直线所成角定义可知所成角为![]() ;根据向量数量积为零可知
;根据向量数量积为零可知![]() ,进而得到
,进而得到![]() ,根据线面垂直性质知
,根据线面垂直性质知![]() ,得到线面垂直关系
,得到线面垂直关系![]() 平面
平面![]() ,由线面垂直性质得
,由线面垂直性质得![]() ,根据长度关系可求得
,根据长度关系可求得![]() ,进而求得异面直线所成角;求得圆锥侧面展开图圆心角后,根据弧长关系可求得
,进而求得异面直线所成角;求得圆锥侧面展开图圆心角后,根据弧长关系可求得![]() ,由余弦定理可求得结果.
,由余弦定理可求得结果.
(1)由题意得:底面圆半径![]()
![]() 圆锥表面积
圆锥表面积![]()
(2)作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]()
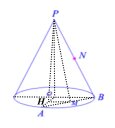
![]() 异面直线
异面直线![]() 与
与![]() 所成角即为
所成角即为![]() 与
与![]() 所成角,即
所成角,即![]()
![]()
![]() ,又
,又![]()
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
又![]() 平面
平面![]()
![]()
![]() 为
为![]() 中点,
中点,![]()
![]() 为
为![]() 中点
中点
![]() ,
,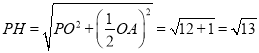
![]()
![]()
即异面直线![]() 与
与![]() 所成角大小为
所成角大小为![]()
由![]() 得:
得:![]() ,即圆锥侧面展开图扇形圆心角为
,即圆锥侧面展开图扇形圆心角为![]()
圆锥侧面展开图如下图所示:
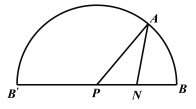
![]()
![]()
![]() 为
为![]() 中点
中点 ![]()
在![]() 中,由余弦定理可得:
中,由余弦定理可得:![]()
![]() ,即
,即![]() 两点在圆锥侧面上的最短距离为
两点在圆锥侧面上的最短距离为![]()


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】如图所示,摩天轮的半径为![]() ,
,![]() 点距地面的高度为
点距地面的高度为![]() ,摩天轮按逆时针方向作匀速运动,且每
,摩天轮按逆时针方向作匀速运动,且每![]() 转一圈,摩天轮上点
转一圈,摩天轮上点![]() 的起始位置在最高点.
的起始位置在最高点.

(1)试确定点![]() 距离地面的高度
距离地面的高度![]() (单位:
(单位:![]() )关于旋转时间
)关于旋转时间![]() (单位:
(单位:![]() )的函数关系式;
)的函数关系式;
(2)在摩天轮转动一圈内,有多长时间![]() 点距离地面超过
点距离地面超过![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 与点
与点![]() 在直线
在直线![]() 的两侧,给出以下结论:①
的两侧,给出以下结论:① ![]() ;② 当
;② 当![]() 时,
时,![]() 有最小值,无最大值;③
有最小值,无最大值;③ ![]() ;④ 当
;④ 当![]() 且
且![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;正确的个数是( )
;正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,点D是A1B的中点,点E是B1C1的中点.
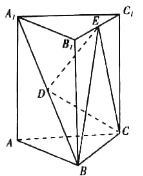
(1)求证:DE∥平面ACC1A1;
(2)若△ABC的面积为![]() ,三棱柱ABC﹣A1B1C1的高为3,求三棱锥D﹣BCE的体积.
,三棱柱ABC﹣A1B1C1的高为3,求三棱锥D﹣BCE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为![]() ,
,![]() ,且小正方形与大正方形面积之比为
,且小正方形与大正方形面积之比为![]() ,则
,则![]() 的值为( )
的值为( )
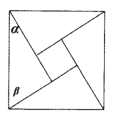
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解儿子身高与其父亲身高的关系,随机调查了5对父子的身高,统计数据如下表所示.
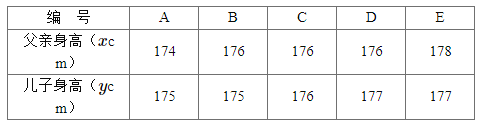
(1)从这五对父子任意选取两对,用编号表示出所有可能取得的结果,并求随机事件M![]() “两对父子中儿子的身高都不低于父亲的身高”发生的概率;
“两对父子中儿子的身高都不低于父亲的身高”发生的概率;
(2)由表中数据,利用“最小二乘法”求![]() 关于
关于![]() 的回归直线的方程.
的回归直线的方程.
参考公式: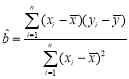 ,
,![]() ;回归直线:
;回归直线:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com