
(本题满分15分) 如图,四边形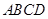 中,
中, 为正三角形,
为正三角形,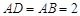 ,
,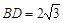 ,
,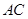 与
与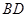 交于
交于 点.将
点.将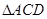 沿边
沿边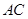 折起,使
折起,使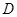 点至
点至 点,已知
点,已知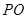 与平面
与平面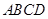 所成的角为
所成的角为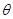 ,且
,且 点在平面
点在平面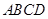 内的射影落在
内的射影落在 内.
内.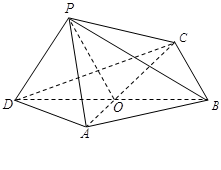
(Ⅰ)求证: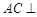 平面
平面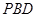 ;
;
(Ⅱ)若已知二面角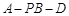 的余弦值为
的余弦值为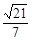 ,求
,求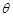 的大小.
的大小.
(Ⅰ)只需证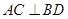 、
、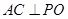 即可;(Ⅱ)
即可;(Ⅱ)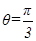 。
。
解析试题分析:(Ⅰ)易知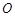 为
为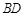 的中点,
的中点,
则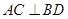 ,又
,又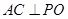 ,
,
又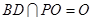 ,
,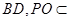 平面
平面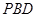 ,
,
所以 平面
平面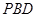 (5分)
(5分)
(Ⅱ)方法一:以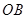 为
为 轴,
轴,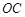 为
为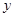 轴,过
轴,过 垂直于
垂直于
平面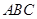 向上的直线为
向上的直线为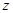 轴建立如图所示空间
轴建立如图所示空间
直角坐标系,则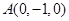 ,
,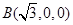
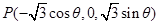 (7分)
(7分)
易知平面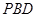 的法向量为
的法向量为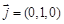 (8分)
(8分)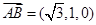 ,
,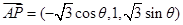 设平面
设平面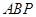 的法向量为
的法向量为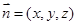
则由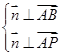 得,
得,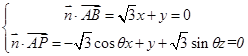
解得,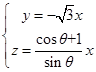 ,令
,令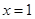 ,则
,则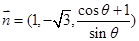 (11分)
(11分)
则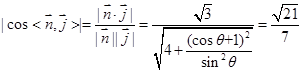
解得,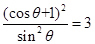 ,即
,即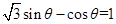 ,即
,即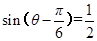 ,
,
又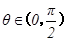 ,∴
,∴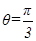 故
故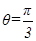 .(15分)
.(15分)
考点:线面垂直的判定定理;线面角;二面角的求法。
点评:用综合法求二面角,往往需要作出平面角,这是几何中一大难点,而用向量法求解二面角无需作出二面角的平面角,只需求出平面的法向量,经过简单运算即可,从而体现了空间向量的巨大作用.二面角的向量求法: ①若AB、CD分别是二面 的两个半平面内与棱
的两个半平面内与棱 垂直的异面直线,则二面角的大小就是向量
垂直的异面直线,则二面角的大小就是向量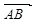 与
与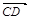 的夹角; ②设
的夹角; ②设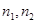 分别是二面角
分别是二面角 的两个面α,β的法向量,则向量
的两个面α,β的法向量,则向量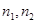 的夹角(或其补角)的大小就是二面角的平面角的大小。
的夹角(或其补角)的大小就是二面角的平面角的大小。


科目:高中数学 来源: 题型:解答题
(本题满分12分)如图,在四棱锥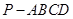 中,底面
中,底面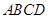 为平行四边形,
为平行四边形,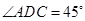 ,
,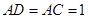 ,
,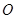 为
为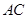 中点,
中点,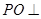 平面
平面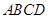 ,
, 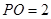 ,
,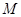 为
为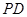 中点.
中点.
(1)证明: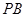 //平面
//平面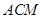 ;
;
(2)证明: 平面
平面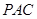 ;
;
(3)求直线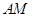 与平面
与平面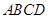 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分11分)
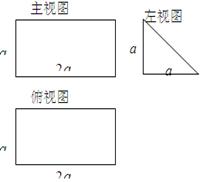
如图示,给出的是某几何体的三视图,其中正视图与侧视图都是边长为2的正三角形,俯视图为半径等于1的圆.试求这个几何体的侧面积与体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)如图,在底面为直角梯形的四棱锥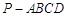 中
中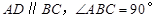 ,
, 平面
平面 ,
,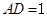 ,
,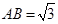 ,
,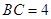 .
.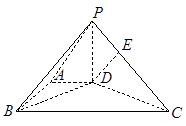
(Ⅰ)求证: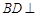
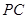 ;
;
(Ⅱ)求直线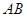 与平面
与平面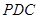 所成的角;
所成的角;
(Ⅲ)设点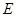 在棱
在棱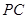 上,
上,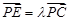 ,若
,若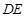 ∥平面
∥平面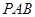 ,求
,求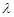 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)一个多面体的直观图和三视图如图所示,其中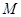 、
、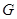 分别是
分别是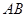 、
、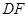 的中点.
的中点.
(1)求证: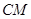
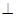 平面
平面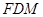
(2)在线段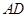 上(含
上(含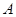 、
、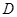 端点)确定一点
端点)确定一点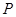 ,使得
,使得
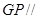 平面
平面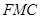 ,并给出证明;
,并给出证明;
(3)一只小飞虫在几何体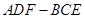 内自由飞,求它飞入几何体
内自由飞,求它飞入几何体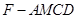 内的概率.
内的概率. 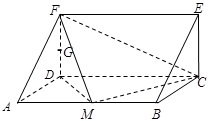
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知梯形ABCD中,AD∥BC,∠ABC ="∠BAD" =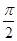 ,AB=BC=2AD=4,
,AB=BC=2AD=4,
E、F分别是AB、CD上的点,且EF∥BC.设AE =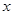 ,G是BC的中点.
,G是BC的中点.
沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
(1)当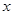 =2时,求证:BD⊥EG ;
=2时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为 ,求
,求 的最大值;
的最大值;
(3)当 取得最大值时,求二面角D-BF-E的余弦值.
取得最大值时,求二面角D-BF-E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知三棱柱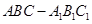 的侧棱与底面垂直,
的侧棱与底面垂直, ,
,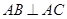 ,
, ,
, 分别是
分别是 ,
, 的中点,点
的中点,点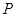 在直线
在直线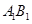 上,且
上,且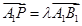 ;
;
(Ⅰ)证明:无论 取何值,总有
取何值,总有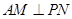 ;
;
(Ⅱ)当 取何值时,直线
取何值时,直线 与平面
与平面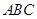 所成的角
所成的角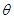 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;
(Ⅲ)是否存在点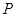 ,使得平面
,使得平面 与平面
与平面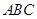 所成的二面角为30º,若存在,试确定点
所成的二面角为30º,若存在,试确定点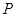 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com