
(本小题满分12分)一个多面体的直观图和三视图如图所示,其中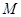 、
、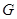 分别是
分别是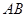 、
、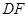 的中点.
的中点.
(1)求证: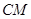
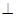 平面
平面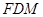
(2)在线段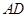 上(含
上(含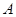 、
、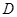 端点)确定一点
端点)确定一点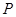 ,使得
,使得
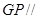 平面
平面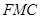 ,并给出证明;
,并给出证明;
(3)一只小飞虫在几何体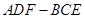 内自由飞,求它飞入几何体
内自由飞,求它飞入几何体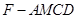 内的概率.
内的概率. 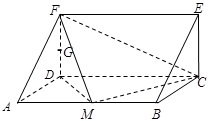
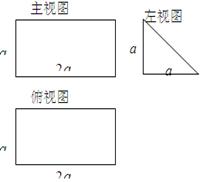
(1)证明见解析(2)证明见解析(3)
解析试题分析:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC
(1) 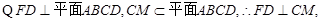
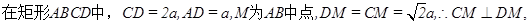
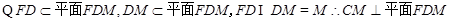 ……4分
……4分
(2)点P在A点处. ……5分
证明:取DC中点S,连接AS、GS、GA
∵G是DF的中点,GS//FC,AS//CM
∴面GSA//面FMC,而GA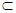 面GSA,∴GP//平面FMC. ……9分
面GSA,∴GP//平面FMC. ……9分
(3)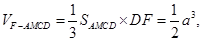
 ,
,
由几何概型知,小虫飞入几何体的概率为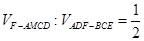 . ……12分
. ……12分
考点:本小题主要考查空间中的平行和垂直的证明和体积的计算以及几何概型求概率问题,考查学生的转化能力和空间想象能力.
点评:证明空间中的平行或垂直问题时,要紧扣定理,条件缺一不可,几何概型主要应该掌握与长度、面积、体积有关的几种.


科目:高中数学 来源: 题型:解答题
如图(1),在等腰直角三角形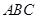 中,
中,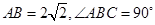 ,点
,点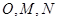 分别为线段
分别为线段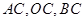 的中点,将
的中点,将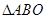 和
和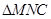 分别沿
分别沿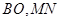 折起,使二面角
折起,使二面角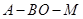 和二面角
和二面角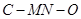 都成直二面角,如图(2)所示。
都成直二面角,如图(2)所示。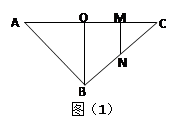

(1)求证: 面
面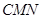 ;
;
(2)求平面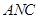 与平面
与平面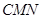 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)求点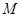 到平面
到平面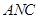 的距离。
的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分15分) 如图,四边形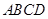 中,
中, 为正三角形,
为正三角形,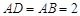 ,
,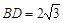 ,
,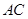 与
与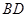 交于
交于 点.将
点.将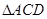 沿边
沿边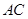 折起,使
折起,使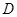 点至
点至 点,已知
点,已知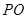 与平面
与平面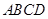 所成的角为
所成的角为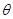 ,且
,且 点在平面
点在平面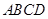 内的射影落在
内的射影落在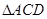 内.
内.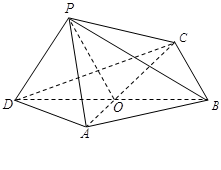
(Ⅰ)求证: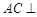 平面
平面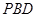 ;
;
(Ⅱ)若已知二面角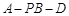 的余弦值为
的余弦值为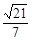 ,求
,求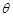 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
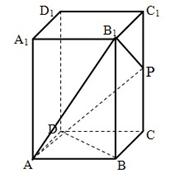
如图,在长方体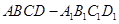 中,
中,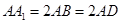 ,且
,且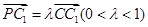 .
.
(I)求证:对任意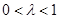 ,总有
,总有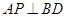 ;
;
(II)若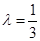 ,求二面角
,求二面角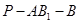 的余弦值;
的余弦值;
(III)是否存在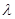 ,使得
,使得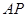 在平面
在平面 上的射影平分
上的射影平分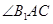 ?若存在, 求出
?若存在, 求出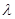 的值, 若不存在,说明理由.
的值, 若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com