
【题目】如图所示,四棱锥![]() 的底面
的底面![]() 是边长为1的菱形,
是边长为1的菱形,![]() ,
,
E是CD的中点,PA![]() 底面ABCD,
底面ABCD,![]() .
.
(I)证明:平面PBE![]() 平面PAB;
平面PAB;
(II)求二面角A—BE—P和的大小.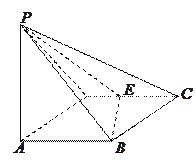
【答案】(I)同解析(II)二面角![]() 的大小为
的大小为![]()
【解析】
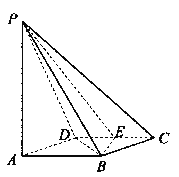
解:解法一(I)如图所示, 连结![]() 由
由![]() 是菱形且
是菱形且![]() 知,
知,
![]() 是等边三角形. 因为E是CD的中点,所以
是等边三角形. 因为E是CD的中点,所以
![]() 又
又![]() 所以
所以![]()
又因为PA![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,
所以![]() 而
而![]() 因此
因此![]() 平面PAB.
平面PAB.
又![]() 平面PBE,所以平面PBE
平面PBE,所以平面PBE![]() 平面PAB.
平面PAB.
(II)由(I)知,![]() 平面PAB,
平面PAB,![]() 平面PAB, 所以
平面PAB, 所以![]()
又![]() 所以
所以![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() .
.
故二面角![]() 的大小为
的大小为![]()
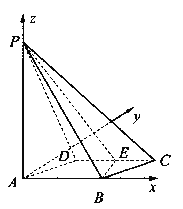
解法二:如图所示,以A为原点,建立空间直角坐标系.则相关各点的坐标分别是
![]()
![]()
![]()
![]()
![]()
![]()
(I)因为![]() 平面PAB的一个法向量是
平面PAB的一个法向量是![]() 所以
所以![]() 和
和![]() 共线.
共线.
从而![]() 平面PAB. 又因为
平面PAB. 又因为![]() 平面PBE,所以平面PBE
平面PBE,所以平面PBE![]() 平面PAB.
平面PAB.
(II)易知![]() 设
设![]()
![]() 是平面PBE的一个法向量,
是平面PBE的一个法向量,
则由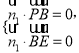 得
得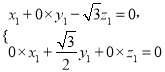 所以
所以![]()
故可取![]()
![]() 而平面ABE的一个法向量是
而平面ABE的一个法向量是![]()
于是,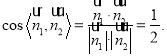 .
.
故二面角![]() 的大小为
的大小为![]()


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:
【题目】越野汽车轮胎的质量是根据其正常使用的时间来衡量,使用时间越长,表明质量越好,且使用时间大于或等于6千小时的为优质品.现用![]() ,
,![]() 两种不同型号的汽车轮胎做试验,各随机抽取部分产品作为样本,得到试验结果的频率分布直方图如图所示,以上述试验结果中各组的频率作为相应的概率.
两种不同型号的汽车轮胎做试验,各随机抽取部分产品作为样本,得到试验结果的频率分布直方图如图所示,以上述试验结果中各组的频率作为相应的概率.

(1)现从大量的![]() ,
,![]() 两种型号的轮胎中各随机抽取2件产品,求其中至少有3件是优质品的概率;
两种型号的轮胎中各随机抽取2件产品,求其中至少有3件是优质品的概率;
(2)通过多年统计发现,![]() 型轮胎每件产品的利润
型轮胎每件产品的利润![]() (单位:元)与其使用时间
(单位:元)与其使用时间![]() (单位:千小时)的关系如下表:
(单位:千小时)的关系如下表:
使用时间 |
|
|
|
每件产品的利润 |
| 200 | 400 |
若从大量的![]() 型轮胎中随机抽取两件,其利润之和记为
型轮胎中随机抽取两件,其利润之和记为![]() (单位:元),求
(单位:元),求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知边长为![]() 米的正方形钢板有一个角被锈蚀,其中
米的正方形钢板有一个角被锈蚀,其中![]() 米,
米, ![]() 米.为了合理利用这块钢板,将在五边形
米.为了合理利用这块钢板,将在五边形![]() 内截取一个矩形块
内截取一个矩形块![]() ,使点
,使点![]() 在边
在边![]() 上.
上.
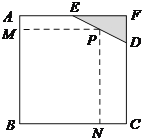
(1)设![]() 米,
米, ![]() 米,将
米,将![]() 表示成
表示成![]() 的函数,求该函数的解析式及定义域;
的函数,求该函数的解析式及定义域;
(2)求矩形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (t为参数).以
(t为参数).以![]() 为极点,x轴的非负半轴为极轴建立极坐标系,曲线
为极点,x轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,则
,则![]() ,
,![]() 满足什么条件时,曲线
满足什么条件时,曲线![]() 与
与![]() 在
在![]() 处总有相同的切线?
处总有相同的切线?
(2)当![]() 时,求函数
时,求函数![]() 的单调减区间;
的单调减区间;
(3)当![]() 时,若
时,若![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①某同学投篮的命中率为0.6,他10次投篮中命中的次数![]() 是一个随机变量,且
是一个随机变量,且![]() ;
;
②某福彩中奖概率为![]() ,某人一次买了8张,中奖张数
,某人一次买了8张,中奖张数![]() 是一个随机变量,且
是一个随机变量,且![]() ;
;
③从装有5个红球、5个白球的袋中,有放回地摸球,直到摸出白球为止,则摸球次数![]() 是随机变量,且
是随机变量,且![]()
A.0个B.1个C.2个D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com