[题目]抛物线的焦点为.准线为.是抛物线上的两个动点.且满足．设线段的中点在上的投影为.则的最大值是 . 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】抛物线的焦点为，准线为，是抛物线上的两个动点，且满足．设线段的中点在上的投影为，则的最大值是_______.

【答案】A

【解析】

试题设|AF|=a，|BF|=b，连接AF、BF．由抛物线定义得2|MN|=a+b，由余弦定理可得|AB|2=（a+b）2﹣3ab，进而根据基本不等式，求得|AB|的取值范围，从而得到本题答案．

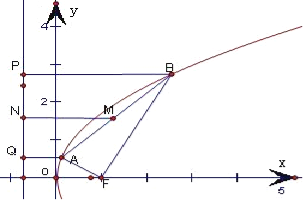
解：设|AF|=a，|BF|=b，连接AF、BF，

由抛物线定义，得|AF|=|AQ|，|BF|=|BP|，

在梯形ABPQ中，2|MN|=|AQ|+|BP|=a+b．

由余弦定理得，

|AB|2=a2+b2﹣2abcos60°=a2+b2﹣ab，

配方得，|AB|2=（a+b）2﹣3ab，

又∵ab≤，

∴（a+b）2﹣3ab≥（a+b）2﹣（a+b）2=（a+b）2

得到|AB|≥（a+b）．

∴≤1，

即的最大值为1．

故选：A．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】若函数在区间[﹣k，k]（k＞0）上的值域为[m，n]，则m+n等于（）
A.0
B.2
C.4
D.6

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知min{{a，b}= f（x）=min{|x|，|x+t|}，函数f（x）的图象关于直线x=﹣ 对称；若“x∈[1，+∞），ex＞2mex”是真命题（这里e是自然对数的底数），则当实数m＞0时，函数g（x）=f（x）﹣m零点的个数为．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】函数f（x）=sin（2x+φ）（|φ＜ |）的图象向左平移个单位后关于原点对称，求函数f（x）在[0， ]上的最小值为（）
A.﹣
B.﹣
C.
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】2017年，嘉积中学即将迎来100周年校庆．为了了解在校同学们对嘉积中学的看法，学校进行了调查，从三个年级任选三个班，同学们对嘉积中学的看法情况如下：

对嘉积中学的看法	非常好，嘉积中学奠定了我一生成长的起点	很好，我的中学很快乐很充实
A班人数比例
B班人数比例
C班人数比例

（Ⅰ）从这三个班中各选一个同学，求恰好有2人认为嘉积中学“非常好”的概率（用比例作为相应概率）；
（Ⅱ）若在B班按所持态度分层抽样，抽取9人，在这9人中任意选取3人，认为嘉积中学“非常好”的人数记为ξ，求ξ的分布列和数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】以表示值域为R的函数组成的集合，表示具有如下性质的函数组成的集合：对于函数，存在一个正数，使得函数的值域包含于区间.例如，当，时，，.现有如下命题：

①设函数的定义域为，则“”的充要条件是“，，”；

②函数的充要条件是有最大值和最小值；

③若函数，的定义域相同，且，，则；

④若函数（，）有最大值，则.

其中的真命题有 .（写出所有真命题的序号）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数的图象上存在不同的两点 ,使得曲线在这两点处的切线重合，则实数的取值范围是（）
A.
B.
C.
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系中，已知曲线：（为参数），以平面直角坐标系的原点为极点，轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线： .
（1）将曲线上的所有点的横坐标、纵坐标分别伸长为原来的、2倍后得到曲线，试写出直线的直角坐标方程和曲线的参数方程；
（2）在曲线上求一点，使点到直线的距离最大，并求出此最大值.