
【题目】如图,等腰直角三角形ABC所在的平面与半圆弧AB所在的平面垂直,AC⊥AB,P是弧AB上一点,且∠PAB=30°.
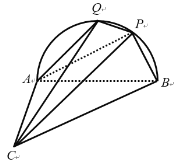
(1)证明:平面BCP⊥平面ACP;
(2)若Q是弧AP上异于AP的一个动点,当三棱锥C-APQ体积最大时,求二面角A-PQ-C的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)根据等腰直角三角形ABC所在的平面与半圆弧AB所在的平面垂直,AC⊥AB,得到![]() 平面APB,从而
平面APB,从而![]() ,又
,又![]() ,由线面垂直的判定定理得到
,由线面垂直的判定定理得到![]() 平面ACP,再由面面垂直的判定定理证明.
平面ACP,再由面面垂直的判定定理证明.
(2)由(1)知![]() 平面APB,若三棱锥C-APQ体积最大,则三角形APQ面积最大,此时
平面APB,若三棱锥C-APQ体积最大,则三角形APQ面积最大,此时![]() 为
为![]() 的中点,过点A作
的中点,过点A作![]() ,连接
,连接![]() ,得到
,得到![]() 平面ACE,从而
平面ACE,从而![]() 为二面角A-PQ-C的平面角,根据∠PAB=30°,设AC=2,求得AE,CE即可.
为二面角A-PQ-C的平面角,根据∠PAB=30°,设AC=2,求得AE,CE即可.
(1)因为等腰直角三角形ABC所在的平面与半圆弧AB所在的平面垂直,AC⊥AB,
所以![]() 平面APB,又PB
平面APB,又PB![]() 平面APB,
平面APB,
所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() 平面ACP,又
平面ACP,又![]() 平面BCP,
平面BCP,
所以平面BCP⊥平面ACP;
(2)由(1)知![]() 平面APB,
平面APB,
所以AC为三棱锥C-APQ的高,设![]()
若三棱锥C-APQ体积最大,则三角形APQ面积最大
当![]() 为
为![]() 的中点时,三角形APQ面积最大,
的中点时,三角形APQ面积最大,
如图所示:
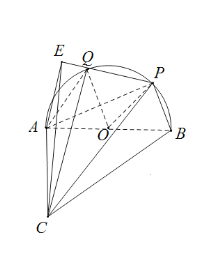
过点A作![]() ,连接
,连接![]() ,
,
所以![]() 平面ACE,
平面ACE,
所以![]() 为二面角A-PQ-C的平面角,
为二面角A-PQ-C的平面角,
因为∠PAB=30°.
所以![]() ,
,
所以![]() ,
,![]()
所以![]() ,
,
所以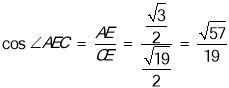 .
.


科目:高中数学 来源: 题型:
【题目】动圆![]() 过定点
过定点![]() ,且在
,且在![]() 轴上截得的弦
轴上截得的弦![]() 的长为4.
的长为4.
(1)若动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(2)在曲线![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使过点
,使过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 的交点
的交点![]() 满足
满足![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标及定值;若不存在,请说明理由.
的坐标及定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年以来,世界经济和贸易增长放缓,中美经贸摩擦影响持续显现,我国对外贸易仍然表现出很强的韧性.今年以来,商务部会同各省市全面贯彻落实稳外贸决策部署,出台了一系列政策举措,全力营造法治化国际化便利化的营商环境,不断提高贸易便利化水平,外贸稳规模提质量转动力取得阶段性成效,进出口保持稳中提质的发展势头,如图是某省近五年进出口情况统计图,下列描述错误的是( )
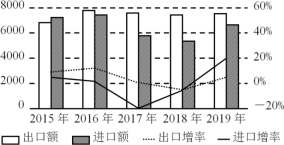
A.这五年,2015年出口额最少B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降D.这五年,2019年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上的点到点
上的点到点![]() 的距离比到直线
的距离比到直线![]() 的距离小
的距离小![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)过点![]() 且倾斜角为
且倾斜角为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的面积;
的面积;
(2)设![]() 为曲线
为曲线![]() 上任意一点,点
上任意一点,点![]() ,是否存在垂直于
,是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在,求出
为直径的圆截得的弦长恒为定值?若存在,求出![]() 的方程和定值;若不存在,说明理由.
的方程和定值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若曲线![]() 在点(1,0)处的切线为l : x+y-1=0,求a,b的值;
在点(1,0)处的切线为l : x+y-1=0,求a,b的值;
(3)若![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com