
【题目】已知曲线C1的极坐标方程为ρcos(θ﹣ ![]() )=﹣1,曲线C2的极坐标方程为ρ=2
)=﹣1,曲线C2的极坐标方程为ρ=2 ![]() cos(θ﹣
cos(θ﹣ ![]() ).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.
).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.
(1)求曲线C2的直角坐标方程;
(2)求曲线C2上的动点M到曲线C1的距离的最大值.
【答案】
(1)解:曲线C2的极坐标方程为ρ=2 ![]() cos(θ﹣
cos(θ﹣ ![]() ),即 ρ2=2
),即 ρ2=2 ![]() ρ(
ρ( ![]() cosθ+
cosθ+ ![]() sinθ),
sinθ),
化为直角坐标方程为 x2+y2=2x+2y,即 (x﹣1)2+(y﹣1)2=2
(2)解:曲线C1的极坐标方程为ρcos(θ﹣ ![]() )=﹣1即
)=﹣1即 ![]() x+
x+ ![]() y=﹣1,即 x+
y=﹣1,即 x+ ![]() y+2=0.
y+2=0.
圆心C2(1,1)到曲线C1的距离为d= ![]() =
= ![]() ,
,
故曲线C2上的动点M到曲线C1的距离的最大值为d+r= ![]() +
+ ![]()
【解析】(1)根据x=ρcosθ,y=ρsinθ,把曲线C2的极坐标方程化为直角坐标方程.(2)把曲线C1的极坐标方程化为直角坐标方程,求得圆心C2(1,1)到曲线C1的距离d的值,则d加上半径,即为所求.


科目:高中数学 来源: 题型:
【题目】为研究质量x(单位:g)对弹簧长度y(单位:cm)的影响,对不同质量的6根弹簧进行测量,得到如下数据:
x (g) | 5 | 10 | 15 | 20 | 25 | 30 |
y (cm) | 7.25 | 8.12 | 8.95 | 9.90 | 10.9 | 11.8 |
(1)画出散点图;
(2)如果散点图中的各点大致分布在一条直线的附近,求y与x之间的回归方程. ( 其中  )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某算法的程序框图如图所示,其中输入的变量![]() 在1,2,3,…,24这24个整数中等可能随机产生.
在1,2,3,…,24这24个整数中等可能随机产生.
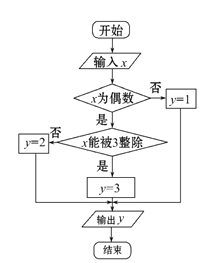
(Ⅰ)分别求出按程序框图正确编程运行时输出![]() 的值为
的值为![]() 的概率
的概率![]() (
(![]() =1,2,3);
=1,2,3);
(Ⅱ)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出![]() 的值为
的值为![]() (
(![]() =1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
运行 次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
30 | 14 | 6 | 10 |
… | … | … | … |
2 100 | 1 027 | 376 | 697 |
乙的频数统计表(部分)
运行 次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
30 | 12 | 11 | 7 |
… | … | … | … |
2 100 | 1 051 | 696 | 353 |
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出![]() 的值为
的值为![]() (
(![]() =1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.
=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.
(Ⅲ)将按程序框图正确编写的程序运行3次,求输出![]() 的值为2的次数ξ的分布列及数学期望.
的值为2的次数ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B是抛物线W: ![]() 上的两个动点,F是抛物线W的焦点,
上的两个动点,F是抛物线W的焦点, ![]() 是坐标原点,且恒有
是坐标原点,且恒有![]() .
.
(1)若直线OA的倾斜角为![]() 时,求线段AB的中点C的坐标;
时,求线段AB的中点C的坐标;
(2)求证直线AB经过一定点,并求出此定点.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒子中有大小相同的球6个,其中标号为1的球2个,标号为2的球3个.标号为3的球1个,第一次从盒子中任取1个球,放回后第二次再任取1个球 (假设取到每个球的可能性都相同).记第一次与第二次取到球的标号之和为ξ.
(1)求随机变量ξ的分布列:
(2)求随机变量ξ的期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校设计了一个实验考察方案:考生从6道备选题中随机抽取3道题,按照题目要求独立完成全部实验操作,规定:至少正确完成其中的2道题便可通过.己知6道备选题中考生甲有4道能正确完成,2道题不能完成;考生乙每题正确完成的概率都是 ![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(I) 求甲考生通过的概率;
(II) 求甲、乙两考生正确完成题数的概率分布列,和甲、乙两考生的数学期望;
(Ⅲ)请分析比较甲、乙两考生的实验操作能力.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com