
【题目】对于![]() 元集合
元集合![]() ,若
,若![]() 元集合
元集合![]() 满足
满足![]() ,且
,且![]() .则称
.则称![]() 是集合
是集合![]() 的一种“等和划分”(
的一种“等和划分”(![]() 与
与![]() 算是同一种划分).试确定集合
算是同一种划分).试确定集合![]() 共有多少种等和划分?
共有多少种等和划分?
【答案】29
【解析】
解法1:不妨设![]() .由于当集合
.由于当集合![]() 确定后,集合
确定后,集合![]() 便唯一确定,故只须考虑集合
便唯一确定,故只须考虑集合![]() 的个数.
的个数.
设![]() 为最大数.由
为最大数.由![]() ,知
,知![]() .于是,
.于是,![]() .故
.故![]() 中有奇数个奇数.
中有奇数个奇数.
(1)若![]() 中有五个奇数,因
中有五个奇数,因![]() 中的六个奇数之和为36,而
中的六个奇数之和为36,而![]() ,所以,
,所以,![]() .此时,得到唯一的
.此时,得到唯一的![]() .
.
(2)若![]() 中有三个奇数、两个偶数,用
中有三个奇数、两个偶数,用![]() 表示
表示![]() 中这两个偶数
中这两个偶数![]() 之和,
之和,![]() 表示
表示![]() 中这三个奇数
中这三个奇数![]() 之和,则
之和,则![]() .于是,
.于是,![]() .共得
.共得![]() 的24种情形.
的24种情形.
①当![]() 时,
时,![]() ,可搭配成
,可搭配成![]() 的3种情形;
的3种情形;
②当![]() 时,
时,![]() ,可搭配成
,可搭配成![]() 的3种情形;
的3种情形;
③当![]() 时,
时,![]() ,可搭配成
,可搭配成![]() 的6种情形;
的6种情形;
④当![]() 时,
时,![]() ,可搭配成
,可搭配成![]() 的6种情形;
的6种情形;
⑤当![]() 时,
时,![]() ,可搭配成
,可搭配成![]() 的4种情形;
的4种情形;
⑥当![]() 时,
时,![]() ,可搭配成
,可搭配成![]() 的1种情形;
的1种情形;
⑦当![]() 时,
时,![]() ,可搭配成
,可搭配成![]() 的1种情形;
的1种情形;
(3)若![]() 中有一个奇数、四个偶数,由于
中有一个奇数、四个偶数,由于![]() 中除12外,其余的五个偶数和为
中除12外,其余的五个偶数和为![]() ,从中去掉一个偶数,补加一个奇数,使
,从中去掉一个偶数,补加一个奇数,使![]() 中五数之和为27,分别得到
中五数之和为27,分别得到![]() 的4种情形
的4种情形![]() .综上,集合
.综上,集合![]() 有
有![]() 种情形.即
种情形.即![]() 有29种等和划分.
有29种等和划分.
解法2:元素交换法.
显然,![]() ,恒设
,恒设![]() .
.
(1)首先注意极端情况的一种分划:
![]() .
.
显然,数组![]() 与
与![]() 中,若有一组数全在
中,若有一组数全在![]() 中,则另一组数必全在
中,则另一组数必全在![]() 中.
中.
以下考虑10、11两个数至少一个不在![]() 中的情况.
中的情况.
为此,考虑![]() 中个数相同且和数相等的元素交换.
中个数相同且和数相等的元素交换.
(2)![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
共得到8种对换.
(3)![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
共得到9种对换.
(4)![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
共得到11种对换.
每种对换都得到一种新的划分.因此,总共得![]() 种等和划分.
种等和划分.


科目:高中数学 来源: 题型:
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,把函数
)的部分图象如图所示,把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像。
的图像。

(1)当![]() 时,若方程
时,若方程![]() 恰好有两个不同的根
恰好有两个不同的根![]() ,求
,求![]() 的取值范围及
的取值范围及![]() 的值;
的值;
(2)令![]() ,若对任意
,若对任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知边长为4的正三角形ABC的边AB、AC上分别有两点D、E,DE//BC且DE=3,现将△ABC沿DE折成直二面角A﹣DE﹣B,在空间中取一点F使得ADBF为平行四边形,连接AC、FC得六面体ABCEDF,G是BC边上动点.
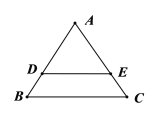
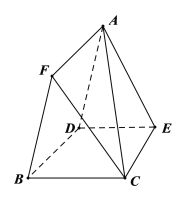
(1)若EG//平面ACF,求CG的长;
(2)若G为BC中点,求二面角G﹣AE﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为![]() 的铁球,并注入水,使水面与球正好相切,然后将球取出,则这时容器中水的深度为___________.
的铁球,并注入水,使水面与球正好相切,然后将球取出,则这时容器中水的深度为___________.
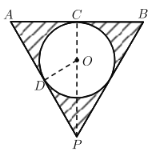
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 个数
个数![]() ,
,![]() ,…,
,…,![]() 的连乘积
的连乘积![]() 记为
记为![]() ,将
,将![]() 个数
个数![]() ,
,![]() ,…,
,…,![]() 的和
的和![]() 记为
记为![]() .(
.(![]() )
)
(1)若数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,求
,求![]() ;
;
(2)用![]() 表示不超过
表示不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() ,
,![]() .若数列
.若数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设定义在正整数集![]() 上的函数
上的函数![]() 满足:当
满足:当![]() (
(![]() )时,
)时,![]() ,问是否存在正整数
,问是否存在正整数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由(已知
的值;若不存在,说明理由(已知![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com