
【题目】在平面直角坐标系中,以原点为极点,x轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线C的极坐标方程为ρ=2cos θ,直线l的参数方程为![]() (t为参数,α为直线的倾斜角).
(t为参数,α为直线的倾斜角).
(1)写出直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C有唯一的公共点,求角α的大小.
【答案】(1)当![]() 时,直线l方程为x=-1;当
时,直线l方程为x=-1;当![]() 时,直线l方程为
时,直线l方程为
y=(x+1)tanα; x2+y2=2x (2)![]() 或
或![]() .
.
【解析】
(1)对直线l的倾斜角分类讨论,消去参数![]() 即可求出其普通方程;由
即可求出其普通方程;由![]() ,即可求出曲线C的直角坐标方程;
,即可求出曲线C的直角坐标方程;
(2)将直线l的参数方程代入曲线C的直角坐标方程,根据条件Δ=0,即可求解.
(1)当![]() 时,直线l的普通方程为x=-1;
时,直线l的普通方程为x=-1;
当![]() 时,消去参数
时,消去参数![]() 得
得
直线l的普通方程为y=(x+1)tan α.
由ρ=2cos θ,得ρ2=2ρcos θ,
所以x2+y2=2x,即为曲线C的直角坐标方程.
(2)把x=-1+tcos α,y=tsin α代入x2+y2=2x,
整理得t2-4tcos α+3=0.
由Δ=16cos2α-12=0,得cos2α=![]() ,
,
所以cos α=![]() 或cos α=
或cos α=![]() ,
,
故直线l的倾斜角α为![]() 或
或![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,原点为
中,原点为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() ,线段
,线段![]() 是抛物线
是抛物线![]() 的一条动弦.
的一条动弦.
(1)求抛物线![]() 的准线方程和焦点坐标
的准线方程和焦点坐标![]() ;
;
(2)当![]() 时,设圆
时,设圆![]() :
:![]() ,若存在两条动弦
,若存在两条动弦![]() ,满足直线
,满足直线![]() 与圆
与圆![]() 相切,求半径
相切,求半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天干地支,简称为干支,源自中国远古时代对天象的观测.“甲、乙、丙、丁、戊、己、庚、辛、壬、癸”称为十天干,“子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥”称为十二地支.干支纪年法是天干和地支依次按固定的顺序相互配合组成,以此往复,60年为一个轮回.现从农历2000年至2019年共20个年份中任取2个年份,则这2个年份的天干或地支相同的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场一年中各月份的收入、支出情况的统计如图所示,下列说法中正确的是______.
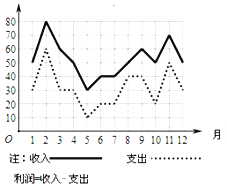
①2至3月份的收入的变化率与11至12月份的收入的变化率相同;
②支出最高值与支出最低值的比是6:1;
③第三季度平均收入为50万元;
④利润最高的月份是2月份。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() ),下列结论正确的是( )
),下列结论正确的是( )
①当![]() 时,
时,![]() 恒成立;②当
恒成立;②当![]() 时,
时,![]() 的零点为
的零点为![]() 且
且![]() ;③当
;③当![]() 时,
时,![]() 是
是![]() 的极值点;④若
的极值点;④若![]() 有三个零点,则实数k的取值范围为
有三个零点,则实数k的取值范围为![]() .
.
A.①②④B.①③C.②③④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() (
(![]() )过点
)过点![]() ,其上顶点为
,其上顶点为![]() ,右顶点和右焦点分别为
,右顶点和右焦点分别为![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点(异于点
两点(异于点![]() ),
),![]() ,试判定直线
,试判定直线![]() 是否过定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
是否过定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com