
【题目】设函数 ![]() ,若函数
,若函数 ![]() 在x=1处与直线
在x=1处与直线 ![]() 相切.
相切.
(Ⅰ)求实数a,b的值;
(Ⅱ)求函数 ![]() 在
在 ![]() 上的最大值.
上的最大值.
【答案】解:(I)f′(x)= ![]() -2bx , ∵函数f(x)在x=1处与直线y=-
-2bx , ∵函数f(x)在x=1处与直线y=- ![]() 相切,
相切,
∴ 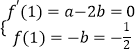 解得
解得 ![]()
(Ⅱ)由(1)知,f(x)=lnx- ![]() x2 , f′(x)=
x2 , f′(x)= ![]() -x=
-x= ![]() ,
,
当 ![]() ≤x≤e时,令f′(x)>0,得
≤x≤e时,令f′(x)>0,得 ![]() ≤x<1,
≤x<1,
令f′(x)<0,得1<x≤e, ∴f(x)在[ ![]() ,1)上是增加的,
,1)上是增加的,
在(1,e]上是减少的, ∴f(x)max=f(1)=- ![]() .
.
【解析】本题主要考查导数的几何意义,切线方程以及导数展示单调性中的应用。(1)求出函数的导数,根据导数的几何意义,根据函数在x=1处于直线相切,列出方程组求解即可。(2)求出函数的导数,根据导数的不等式及性质,判断函数的单调性,进而求出函数在闭区间上的最值。
【考点精析】关于本题考查的导数的几何意义和函数的最大(小)值与导数,需要了解通过图像,我们可以看出当点![]() 趋近于
趋近于![]() 时,直线
时,直线![]() 与曲线相切.容易知道,割线
与曲线相切.容易知道,割线![]() 的斜率是
的斜率是![]() ,当点
,当点![]() 趋近于
趋近于![]() 时,函数
时,函数![]() 在
在![]() 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即![]() ;求函数
;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆Ω: ![]() 的离心率为
的离心率为 ![]() ,直线l:y=2上的点和椭圆Ω上的点的距离的最小值为1.
,直线l:y=2上的点和椭圆Ω上的点的距离的最小值为1.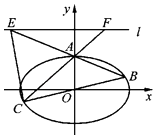
(Ⅰ) 求椭圆Ω的方程;
(Ⅱ) 已知椭圆Ω的上顶点为A,点B,C是Ω上的不同于A的两点,且点B,C关于原点对称,直线AB,AC分别交直线l于点E,F.记直线AC与AB的斜率分别为k1 , k2
①求证:k1k2为定值;
②求△CEF的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点![]() 为圆心的圆过点
为圆心的圆过点![]() 和
和![]() ,线段
,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,
,
(1)求直线![]() 的方程; (2)求圆
的方程; (2)求圆![]() 的方程。
的方程。
(3)设点![]() 在圆
在圆![]() 上,试探究使
上,试探究使![]() 的面积为 8 的点
的面积为 8 的点![]() 共有几个?证明你的结论
共有几个?证明你的结论
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)一个盒子里装有三张卡片,分别标记有数字![]() ,
,![]() ,
,![]() ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取![]() 次,每次抽取
次,每次抽取![]() 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求“抽取的卡片上的数字满足![]() ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的数字![]() ,
,![]() ,
,![]() 不完全相同”的概率.
不完全相同”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
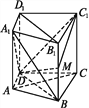
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
(1)求证:B1D1∥平面A1BD;
(2)求证:MD⊥AC;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理:“幂势既同,则积不容异”,它是中国古代一个涉及几何体体积问题,意思是两个等高的几何体,如在同高处的截面积恒相等,则体积相等,设A,B为两个等高的几何体,p:A,B的体积相等,q:A,B在同高处的截面积不恒相等,根据祖暅原理可知,q是-p的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com