Question

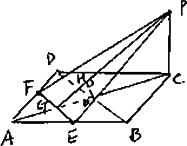
已知：如图，ABCD是边长为2的正方形，PC⊥面ABCD，PC＝2，E、F是AB、AD中点．求：点B到平面PEF的距离．

Answer 1

答案：
解析：

解析：由BD∥EF可证DB∥平面PEF，则点B到平面PEF的距离转化为直线与平面PEF的距离．又由平面PCA垂直平面PEF，故DB与AC的交点到两垂直平面的交线的距离为所求距离． 　　方法一：连接DB，AC交于O点，设AC交EF于G，连PG， 　　作OH⊥PG，H为垂足． 　　∵E、F是AB、AD中点，∴EF∥DB，∴DB∥面PEF， 　　∵ABCD是正方形，∴AC⊥BD，∴EF⊥AC， 　　∵PC⊥面ABCD，∴EF⊥PC，∴EF⊥面PCG， 　　∵EFÌ 面PEF，∴面PEF⊥面PCG， 　　∵OH⊥PG，∴OH⊥面PEF，即OH为所求点B到平面PEF的距离． 　　由ABCD边长为2，∴AC＝2，GO＝，GC＝， 　　∵PC⊥面ABCD，∴PC⊥AC， 　　∴△OHG∽△PCG，∴， 　　由PC＝2，PG＝ 　　∴OH＝＝ 　　即点B到平面PEF的距离为． 　　方法二：如图，连接BF、PB，设点B到平面PEF的距离为d， 　　由VP－BEF＝S△BEF·PC 　　＝××BE×AF×PC 　　＝×1×1×2＝ 　　连AC交EF于G，连PG，由方法一知 　　PG＝，EF＝，S△PEF＝××＝ 　　∴VB－PEF＝·S△PEF·d＝VP－BEF＝， 　　∴d＝1d＝ 　　即点B到平面PEF的距离为．