
(1)已知动点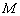 到点
到点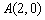 的距离是它到点
的距离是它到点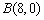 的距离的一半.求动点
的距离的一半.求动点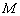 的轨迹方程;
的轨迹方程;
 (2)若A、B是圆C:
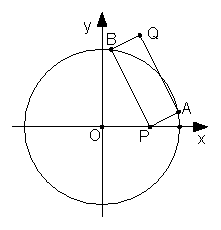
(2)若A、B是圆C: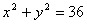 上的两个动点,点P(4,0),满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程
上的两个动点,点P(4,0),满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程
(1)设动点M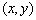 为轨迹上任意一点,则点M的轨迹就是集合
为轨迹上任意一点,则点M的轨迹就是集合
P 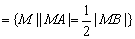 .由两点距离公式,点M适合的条件可表示为
.由两点距离公式,点M适合的条件可表示为
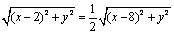 ,平方后再整理,得
,平方后再整理,得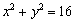 .可以验证,这就是动点M的轨迹方程.
.可以验证,这就是动点M的轨迹方程.
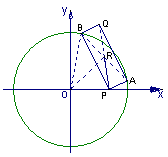 解:设AB的中点为R,坐标为(x,y),则在Rt△ABP中,|AR|=|PR|
解:设AB的中点为R,坐标为(x,y),则在Rt△ABP中,|AR|=|PR|
又因为R是弦AB的中点,依垂径定理 在Rt△OAR中,|AR|2=|AO|2-|OR|2=36-(x2+y2)
又|AR|=|PR|=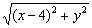
所以有(x-4)2+y2=36-(x2+y2),即x2+y2-4x-10=0
因此点R在一个圆上,而当R在此圆上运动时,Q点即在所求的轨迹上运动
设Q(x,y),R(x1,y1),因为R是PQ的中点,所以x1= ,
,
代入方程x2+y2-4x-10=0,得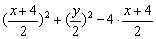 -10=0
-10=0
整理得 x2+y2=56,这就是所求的轨迹方程


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省高三5月高考模拟考试理科数学试卷(解析版) 题型:解答题
已知动点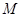 到点
到点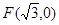 的距离与到直线
的距离与到直线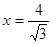 的距离之比为定值
的距离之比为定值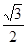 ,记
,记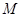 的轨迹为
的轨迹为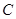 .
.

(1)求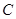 的方程,并画出
的方程,并画出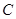 的简图;
的简图;
(2)点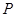 是圆
是圆 上第一象限内的任意一点,过
上第一象限内的任意一点,过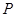 作圆的切线交轨迹
作圆的切线交轨迹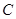 于
于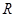 ,
,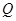 两点.
两点.
(i)证明: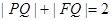 ;
;
(ii)求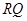 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2013届河北省高二下学期第一次考试理科数学试卷 题型:解答题
已知动点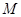 到点
到点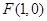 的距离,等于它到直线
的距离,等于它到直线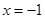 的距离.
的距离.
(1)求点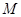 的轨迹
的轨迹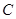 的方程;
的方程;
(2)过点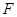 任意作互相垂直的两条直线
任意作互相垂直的两条直线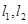 ,分别交曲线
,分别交曲线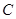 于点
于点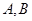 和
和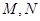 .
.
设线段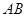 ,
,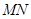 的中点分别为
的中点分别为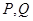 ,求证:直线
,求证:直线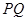 恒过一个定点;
恒过一个定点;
(3)在(2)的条件下,求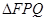 面积的最小值
面积的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
已知动点![]() 到点
到点![]() 的距离等于它到直线
的距离等于它到直线![]() 的距离.
的距离.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .
.
设线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点.
恒过一个定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com