
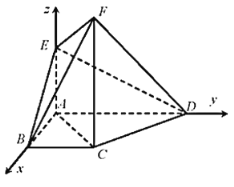
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
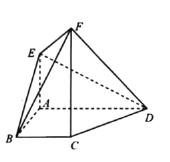
(1)求证:![]() ;
;
(2)若二面角![]() 是直二面角,求
是直二面角,求![]() .
.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接![]() ,证得
,证得![]() ,再由
,再由![]() ,得到
,得到![]() ,进而证得
,进而证得![]() 平面
平面![]() ,即可得到
,即可得到![]() ;
;
(2)以A为原点,![]() 、
、![]() 、
、![]() 分别为x轴、y轴、z轴正方向,建立空间直角坐标系,设
分别为x轴、y轴、z轴正方向,建立空间直角坐标系,设![]() ,分别求得平面
,分别求得平面![]() 和平面
和平面![]() 的法向量
的法向量![]() ,结合
,结合![]() ,求得
,求得![]() 的值,即可求解.
的值,即可求解.
(1)连接![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,可得
,可得![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,所以A,C,F,E四点共面,
,所以A,C,F,E四点共面,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)如图所示,以A为原点,![]() 、
、![]() 、
、![]() 分别为x轴、y轴、z轴正方向,
分别为x轴、y轴、z轴正方向,
建立空间直角坐标系,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
则![]() ,
,![]() ,
,
![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,则
,则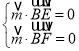 ,
,
即 ,取
,取![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则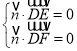 ,
,
即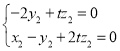 ,取
,取![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
由二面角![]() 是直二面角,则
是直二面角,则![]() ,即
,即![]() ,解得
,解得![]() .
.
所以![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() :
: ![]() 上,
上, ![]() 是椭圆的一个焦点.
是椭圆的一个焦点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)椭圆C上不与![]() 点重合的两点
点重合的两点![]() ,
, ![]() 关于原点O对称,直线
关于原点O对称,直线![]() ,
, ![]() 分别交
分别交![]() 轴于
轴于![]() ,
, ![]() 两点.求证:以
两点.求证:以![]() 为直径的圆被直线
为直径的圆被直线![]() 截得的弦长是定值.
截得的弦长是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《普通高中数学课程标准(2017版)》提出了数学学科的六大核心素养.为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为5分,分值高者为优),则下面叙述正确的是( )
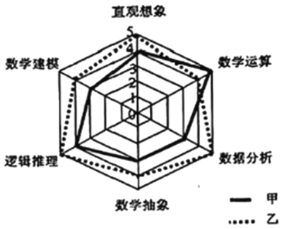
A.甲的数据分析素养高于乙
B.甲的数学建模素养优于数学抽象素养
C.乙的六大素养中逻辑推理最差
D.乙的六大素养整体平均水平优于甲
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】万众瞩目的第14届全国冬季运动运会(简称“十四冬”)于2020年2月16日在呼伦贝尔市盛大开幕,期间正值我市学校放寒假,寒假结束后,某校工会对全校100名教职工在“十四冬”期间每天收看比赛转播的时间作了一次调查,得到如图频数分布直方图:
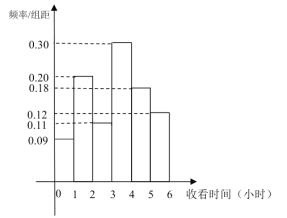
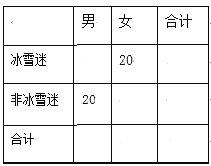
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“冰雪迷”,否则定义为“非冰雪迷”,请根据频率分布直方图补全![]() 列联表;并判断能否有
列联表;并判断能否有![]() 的把握认为该校教职工是否为“冰雪迷”与“性别”有关;
的把握认为该校教职工是否为“冰雪迷”与“性别”有关;
(2)在全校“冰雪迷”中按性别分层抽样抽取6名,再从这6名“冰雪迷”中选取2名作冰雪运动知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
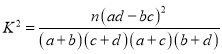 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”
”
B.命题“存在![]() ,使得
,使得![]() ”的否定是:“对任意
”的否定是:“对任意![]() ,均有
,均有![]() ”
”
C.命题“角![]() 的终边在第一象限角,则
的终边在第一象限角,则![]() 是锐角”的逆否命题为真命题
是锐角”的逆否命题为真命题
D.已知![]() 是
是![]() 上的可导函数,则“
上的可导函数,则“![]() ”是“
”是“![]() 是函数
是函数![]() 的极值点”的必要不充分条件
的极值点”的必要不充分条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com