
【题目】已知函数f(x)= ![]() 是定义在(﹣1,1)上的奇函数,且f(1)=1.
是定义在(﹣1,1)上的奇函数,且f(1)=1.
(1)求函数f(x)的解析式;
(2)判断并证明f(x)在(﹣1,1)上的单调性.
【答案】
(1)解:∵函数f(x)= ![]() 是定义在(﹣1,1)上的奇函数,
是定义在(﹣1,1)上的奇函数,
∴f(0)=0,
又∵f(1)=1.
∴ 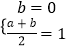 ,
,
解得: ![]() ,
,
∴函数f(x)= ![]()
(2)解:f(x)在(﹣1,1)上单调递增,理由如下:
∵f′(x)= ![]() ,
,
当x∈(﹣1,1)时,f′(x)≥0恒成立,
故f(x)在(﹣1,1)上单调递增
【解析】(1)根据奇函数的特性,可得f(0)=0,结合f(1)=1,构造方程组,解得函数f(x)的解析式;(2)利用导数法,可证得f(x)在(﹣1,1)上单调递增.
【考点精析】本题主要考查了函数单调性的判断方法和利用导数研究函数的单调性的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某工厂的污水处理程序如下:原始污水必先经过A系统处理,处理后的污水(A级水)达到环保标准(简称达标)的概率为![]() .经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
.经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
某厂现有![]() 个标准水量的A级水池,分别取样、检测. 多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
个标准水量的A级水池,分别取样、检测. 多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
现有以下四种方案,
方案一:逐个化验;
方案二:平均分成两组化验;
方案三:三个样本混在一起化验,剩下的一个单独化验;
方案四:混在一起化验.
化验次数的期望值越小,则方案的越“优”.
(Ⅰ) 若![]() ,求
,求![]() 个A级水样本混合化验结果不达标的概率;
个A级水样本混合化验结果不达标的概率;
(Ⅱ) 若![]() ,现有
,现有![]() 个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
(Ⅲ) 若“方案三”比“方案四”更“优”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .数列
.数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 能否为等差数列?若能,求其通项公式;若不能,试说明理由;
能否为等差数列?若能,求其通项公式;若不能,试说明理由;
(3)若数列![]() 是各项均为正整数的递增数列,设
是各项均为正整数的递增数列,设![]() ,则当
,则当![]() ,
, ![]() ,
, ![]() 和
和![]() ,
, ![]() ,
, ![]() 均成等差数列时,求正整数
均成等差数列时,求正整数![]() ,
, ![]() ,
, ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为对数函数,并且它的图象经过点(2 ![]() ,
, ![]() ),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
(1)求函数f(x)的解析式;
(2)求函数y=g(x)在区间[ ![]() ,16]上的最小值.
,16]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式 ![]() <0的解集为( )
<0的解集为( )
A.(﹣1,0)∪(1,+∞)
B.(﹣∞,﹣1)∪(0,1)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣1,0)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(4x+1)﹣x,g(x)=log2a+log2(2x﹣ ![]() )(a>0,x>1).
)(a>0,x>1).
(1)证明函数f(x)为偶函数;
(2)若函数f(x)﹣g(x)只有一个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)=  ,其中x是仪器的月产量.(注:总收益=总成本+利润)
,其中x是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润x表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com