
已知函数f(x)=ln(1+x)-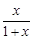 .
.
(1)求f(x)的极小值; (2)若a、b>0,求证:lna-lnb≥1-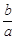 .
.
(1) 0. (2) f(x)≥f(0)=0,从而ln(1+x)≥ 在x>-1时恒成立.令1+x=
在x>-1时恒成立.令1+x= >0,则
>0,则 =1-
=1-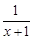 =1-
=1-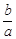 ,于是lna-lnb=ln
,于是lna-lnb=ln ≥1-
≥1-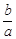 ,即lna-lnb≥1-
,即lna-lnb≥1-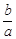 在a>0,b>0时成立.
在a>0,b>0时成立.
【解析】
试题分析:(1)
f(x)=ln(1+x)- ,求导数得
,求导数得
f′(x)=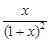 ,而f(x)的定义域x>-1,在x>0时,f′(x)>0;在-1<x<0时,f′(x)<0.
,而f(x)的定义域x>-1,在x>0时,f′(x)>0;在-1<x<0时,f′(x)<0.
∴在x=0时,f(x)取得极小值f(0)=0. 6分
(2)证明:在x=0时,f(x)取得极小值,而且是最小值,于是f(x)≥f(0)=0,从而ln(1+x)≥ 在x>-1时恒成立.
在x>-1时恒成立.
令1+x= >0,则
>0,则 =1-
=1-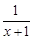 =1-
=1-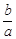 ,
,
于是lna-lnb=ln ≥1-
≥1-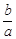 ,
,
因此lna-lnb≥1-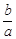 在a>0,b>0时成立.
12分
在a>0,b>0时成立.
12分
考点:本题考查了导数的运用
点评:导数本身是个解决问题的工具,是高考必考内容之一,高考往往结合函数甚至是实际问题考查导数的应用,求单调、最值、完成证明等,请注意归纳常规方法和常见注意点.


科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 3 |
| 2 |
| f′(x) |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| e |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com