
����Ŀ�������й滮�������������������½�סլҪ�ƹ�����ƣ�ԭ���ϲ��ٽ�����סլС�����ѽ��ɵķ��С���͵�λ��ԺҪ���������Ϣ������һʯ����ǧ���ˣ�����˵����һ����.ij��վΪ�˽����ԡ�����С������ͬ���![]() �����Ⱥ�������ȡ��
�����Ⱥ�������ȡ��![]() �˽����ʾ����飬���������˸�������ε�Ƶ�ʷֲ�ֱ��ͼ�����֣���ͼ��ʾ��ͬʱ��
�˽����ʾ����飬���������˸�������ε�Ƶ�ʷֲ�ֱ��ͼ�����֣���ͼ��ʾ��ͬʱ��![]() �˶��⡰����С������ͬ�������ͳ�Ƶõ��±���
�˶��⡰����С������ͬ�������ͳ�Ƶõ��±���

�������������Ƶ�ʷֲ�ֱ��ͼ������![]() ��ֵ��
��ֵ��
���������![]() ����������еġ���ͬ����Ⱥ�У����ֲ�����ķ�����ȡ6�˲�����̸�ᣬȻ�����6���������ȡ2������һ�����飬����2�˵����䶼��
����������еġ���ͬ����Ⱥ�У����ֲ�����ķ�����ȡ6�˲�����̸�ᣬȻ�����6���������ȡ2������һ�����飬����2�˵����䶼��![]() �ڵĸ��� .
�ڵĸ��� .
���𰸡���1��60����2��![]()
����������������1������ֱ��ͼ�У�ÿ��С���ε������Ϊ![]() ���ɵõڶ�����ε�Ƶ�ʣ��������ɵ�Ƶ�ʷֲ�ֱ��ͼ�еڶ�����εĸ����Ӷ��ɵ�������ֱ��ͼ������ֱ��ͼ����������ݿɵ�
���ɵõڶ�����ε�Ƶ�ʣ��������ɵ�Ƶ�ʷֲ�ֱ��ͼ�еڶ�����εĸ����Ӷ��ɵ�������ֱ��ͼ������ֱ��ͼ����������ݿɵ�![]() ��ֵ���ɣ�1��֪��
��ֵ���ɣ�1��֪��![]() ����������е�����ͬ�������ֱ�Ϊ
����������е�����ͬ�������ֱ�Ϊ![]() �ˣ�
�ˣ�![]() �ˣ���˰��շֲ������ȡ6��ʱ����������ε������ֱ�Ϊ4�ˣ�2�ˣ��ɹŵ�����ʹ�ʽ�ɵý��.
�ˣ���˰��շֲ������ȡ6��ʱ����������ε������ֱ�Ϊ4�ˣ�2�ˣ��ɹŵ�����ʹ�ʽ�ɵý��.
�������1��������֪���ڶ����Ƶ��Ϊ![]() .
.
���ԣ�Ƶ�ʷֲ�ֱ��ͼ�еڶ�����ʾ���εĸ�Ϊ![]() ��
��
������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
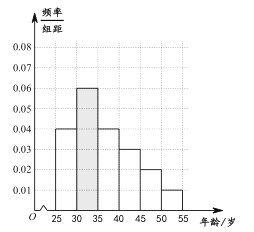
��һ������Ϊ![]() �ˣ�Ƶ��Ϊ
�ˣ�Ƶ��Ϊ![]() ����
����![]() ��.
��.
�ڶ�������Ϊ![]() �ˣ�
�ˣ�![]()
����������Ϊ![]() �ˣ���ͬ����
�ˣ���ͬ����![]() ��.
��.
��2���ɣ�1��֪��![]() ����������еġ���ͬ�������ֱ�Ϊ
����������еġ���ͬ�������ֱ�Ϊ![]() �ˣ�
�ˣ�![]() �ˣ���˰��շֲ������ȡ6��ʱ����������ε������ֱ�Ϊ4�ˣ�2�ˣ�����������Ϊ
�ˣ���˰��շֲ������ȡ6��ʱ����������ε������ֱ�Ϊ4�ˣ�2�ˣ�����������Ϊ![]() .
.


 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Իع鷽�̶�Ӧ��ֱ��![]() ���پ������������ݵ�
���پ������������ݵ�![]() �е�һ���㣻
�е�һ���㣻
�����������������������Խǿ�������ϵ���ľ���ֵԽ�ӽ���![]() ��
��
����ij������У��������![]() ������̬�ֲ�
������̬�ֲ�![]()
![]() ����
����![]() �����
λ������![]() �ڵĸ���Ϊ
�ڵĸ���Ϊ![]() ����
����![]() �����
λ������![]() �ڵĸ���Ϊ
�ڵĸ���Ϊ![]() ��
��
�ܶԷ������![]() ��
��![]() ���������K2�Ĺ۲�ֵk��˵��kԽС���жϡ�
���������K2�Ĺ۲�ֵk��˵��kԽС���жϡ�![]() ��
��![]() �й�ϵ���İ���Խ������������������Ϊ( )
�й�ϵ���İ���Խ������������������Ϊ( )
A. �٢� B. �ڢ� C. �٢� D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
�� ![]() Ϊ��Ȼ�����ĵ�������������
Ϊ��Ȼ�����ĵ�������������![]() �ڵ�
�ڵ�![]() ��������ƽ����
��������ƽ����![]() ��.
��.
��1����![]() ��ֵ��
��ֵ��
��2������![]() �ļ�ֵ.
�ļ�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={x|x2��2x��3��0��x��R}��B={x|m��1��x��m+1��x��R��m��R}
��1����A��B=[1��3]����ʵ��m��ֵ��
��2����ARB����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�Բ![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��![]() Ϊ��������������ԭ��Ϊ���㣬
Ϊ��������������ԭ��Ϊ���㣬![]() ���������Ϊ���ᣬ����������ϵ����������ϵ��ȡ��ͬ�ĵ�λ���ȣ�ֱ��
���������Ϊ���ᣬ����������ϵ����������ϵ��ȡ��ͬ�ĵ�λ���ȣ�ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]()
��1����![]() ʱ���ж�ֱ��
ʱ���ж�ֱ��![]() ��Բ
��Բ![]() �Ĺ�ϵ��
�Ĺ�ϵ��
��2����![]() ������ֻ��һ�㵽ֱ��
������ֻ��һ�㵽ֱ��![]() �ľ������
�ľ������![]() ʱ����
ʱ����![]() �ϵ�ֱ��
�ϵ�ֱ��![]() ����Ϊ
����Ϊ![]() �ĵ�����꣮
�ĵ�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
�� ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
�� ![]() ����Ϊ
����Ϊ![]() ���϶���Ϊ
���϶���Ϊ![]() ��
�� ![]() �����Ϊ
�����Ϊ![]() .
.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����ֱ��![]() ��
�� ![]() ����Բ
����Բ![]() �ཻ�ڲ�ͬ������
�ཻ�ڲ�ͬ������![]() ��
�� ![]() ��
�� ![]() ���߶�
���߶�![]() ���е�.��������
���е�.��������![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() ��ֱ�ڵ�
��ֱ�ڵ�![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ����f��x��=mn�� ��I����f��x���ĵ����������䣻
����f��x��=mn�� ��I����f��x���ĵ����������䣻
��II����֪��ABC�����ڽ�A��B��C�Ա߷ֱ�Ϊa��b��c����a=3��f ![]() ��sinC=2sinB����A��c��b��ֵ��
��sinC=2sinB����A��c��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x��lnx��2ax����������ֵ�㣬��ʵ��a��ȡֵ��Χ�ǣ� ��
A.�����ޣ� ![]() ��
��
B.��0�� ![]() ��
��
C.��0�� ![]() ��
��
D.�� ![]() ��+�ޣ�
��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��С�ס�����λͬѧ�����Ҳ��Ż�ץ��ÿ������ץ1�������ץ3���涨˭ץ�����һ����˭Ӯ. �������ץ����ô�����ƶ���ȷ���ǣ� ��
��С�ס�����λͬѧ�����Ҳ��Ż�ץ��ÿ������ץ1�������ץ3���涨˭ץ�����һ����˭Ӯ. �������ץ����ô�����ƶ���ȷ���ǣ� ��
A. ��![]() =4������б�Ӯ�IJ��� B. ��
=4������б�Ӯ�IJ��� B. ��![]() =6�������б�Ӯ�IJ���
=6�������б�Ӯ�IJ���
C. ��![]() =9������б�Ӯ�IJ��� D. ��
=9������б�Ӯ�IJ��� D. ��![]() =11�������б�Ӯ�IJ���
=11�������б�Ӯ�IJ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com