
����Ŀ��Ϊ���С��¿��á���ѧ����ij��ѧ��ʦ�ֱ��ô�ͳ��ѧ�͡��¿��á����ֲ�ͬ�Ľ�ѧ��ʽ���ڼס��������༶�н��н�ѧʵ�飬Ϊ�˱ȽϽ�ѧЧ�������п��Ժֱ�������༶�и������ȡ20��ѧ���ijɼ�����ͳ�ƣ������ľ�Ҷͼ����ͼ���dzɼ�������70����Ϊ���ɼ���������
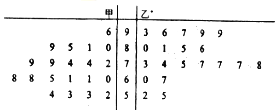
��1���ֱ����ס�������20�������У���ѧ����ǰʮ��ƽ���֣��������ж����ֽ�ѧ��ʽ�Ľ�ѧЧ�����ѣ�
��2��������ͳ��������д����![]() �����������ж��ܷ��ڷ�����ĸ��ʲ�����0��05��ǰ������Ϊ���ɼ��������ѧ��ʽ�йء���
�����������ж��ܷ��ڷ�����ĸ��ʲ�����0��05��ǰ������Ϊ���ɼ��������ѧ��ʽ�йء���
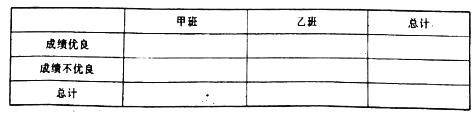
�����ο���ʽ�� 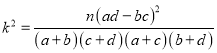 ������
������![]() ��
��
�ٽ�ֵ����
| 0��10 | 0��05 | 0��025 | 0��010 |
| 2��706 | 3��841 | 5��024 | 6��635 |
���𰸡���1�����¿��á���ѧ��ʽ�Ľ�ѧЧ�����ѣ�2����
���������������: ��1���ֱ������װ���Ұ��ƽ���ɼ�,�Ƚϴ�С�ó�����;��2������![]() �ļ��㹫ʽ�ó��۲�ֵ,���ٽ���е�ֵ���жԱ�,�ó�����.
�ļ��㹫ʽ�ó��۲�ֵ,���ٽ���е�ֵ���жԱ�,�ó�����.
�������:��1���װ�������ѧ�ɼ�ǰʮ��ƽ����Ϊ![]()
�Ұ�������ѧ�ɼ�ǰʮ��ƽ����Ϊ![]()
�װ�������ѧ�ɼ�ǰʮ��ƽ����Զ�����Ұ�������ѧ�ɼ�ǰʮ��ƽ���֣����¿����жϡ��¿��á���ѧ��ʽ�Ľ�ѧЧ�����ѣ�
��2���������������£�

����![]() �������е����ݣ���
�������е����ݣ���![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]()
�����ڷ�����ĸ��ʲ�����0��05��ǰ������Ϊ���ɼ��������ѧ��ʽ�йء���


 �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ���ƻ���ֲij�������Ϊ�˶��������������Ʒ�����ֱ��ΪƷ�ּ�Ʒ�������������������ѡȡ�����أ�ÿ���طֳ�![]() С��أ����ܹ�
С��أ����ܹ�![]() С����У����ѡ
С����У����ѡ![]() С�����ֲƷ�ּף�����
С�����ֲƷ�ּף�����![]() С�����ֲƷ������
С�����ֲƷ������
��1������![]() �����һ���ض���ֲƷ�ּĸ��ʣ�
�����һ���ض���ֲƷ�ּĸ��ʣ�
��2������ʱÿ���طֳ�![]() С�飬��
С�飬��![]() �����������õ�Ʒ�ּ�Ʒ�����ڸ�С����ϵ�ÿ�����������λ��kg/hm2�����±���
�����������õ�Ʒ�ּ�Ʒ�����ڸ�С����ϵ�ÿ�����������λ��kg/hm2�����±���
�� |
|
|
|
|
|
|
|
|
�� |
|
|
|
|
|
|
|
|
�ֱ���Ʒ�ּ�Ʒ���ҵ�ÿ�������������ƽ�����������������������������ΪӦ����ֲ��һƷ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڲ����У������Ѷȵļ��㹫ʽΪ![]() ������
������![]() ��
Ϊ��![]() ����Ѷȣ�
����Ѷȣ� ![]() Ϊ��Ը����������
Ϊ��Ը���������� ![]() Ϊ�μӲ��Ե����������ֶ�ijУ�����꼶240��ѧ������һ�β��ԣ���5�����⣬����ǰ���ݶ�ѧ�����˽⣬Ԥ����ÿ������Ѷȣ������ʾ��
Ϊ�μӲ��Ե����������ֶ�ijУ�����꼶240��ѧ������һ�β��ԣ���5�����⣬����ǰ���ݶ�ѧ�����˽⣬Ԥ����ÿ������Ѷȣ������ʾ��
��� | 1 | 2 | 3 | 4 | 5 |
��ǰԤ���Ѷ� | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
���Ժ��������ȡ��20��ѧ���Ĵ������ݽ���ͳ�ƣ���������

�������������ݣ�������240��ѧ���е�5���ʵ����������
���ӳ�����20��ѧ���������ȡ2��ѧ��������2��ѧ���е�5���Ե�����Ϊ![]() ����
����![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
���������Ԥ���ѶȺ�ʵ���Ѷ�֮�����ƫ���![]() Ϊ��
Ϊ��![]() ���ʵ���Ѷȣ�����
���ʵ���Ѷȣ�����![]() ��
��![]() ���һ��ͳ���������ƶ�һ�������жϱ��β��Զ��Ѷȵ�Ԥ���Ƿ������
���һ��ͳ���������ƶ�һ�������жϱ��β��Զ��Ѷȵ�Ԥ���Ƿ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
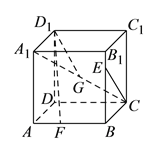
����Ŀ����֪������![]() ����
����![]() ��
�� ![]() ��
�� ![]() �ֱ����߶�
�ֱ����߶�![]() ��
�� ![]() ��
��![]() �ϵĶ��㣬�۲�ֱ��
�ϵĶ��㣬�۲�ֱ��![]() ��
��![]() ��
�� ![]() ��
��![]() ���������н��ۣ�
���������н��ۣ�
�ٶ�����������ĵ�![]() �����ڵ�
�����ڵ�![]() ��ʹ��
��ʹ��![]() ��
��
�ڶ�����������ĵ�![]() �����ڵ�
�����ڵ�![]() ��ʹ��
��ʹ��![]() ��
��
�۶�����������ĵ�![]() �����ڵ�
�����ڵ�![]() ��ʹ��
��ʹ��![]() ��
��
�ܶ�����������ĵ�![]() �����ڵ�
�����ڵ�![]() ��ʹ��
��ʹ��![]() ��
��
������ȷ���۵ĸ����ǣ� ����
A. ![]() �� B.
�� B. ![]() �� C.
�� C. ![]() �� D.
�� D. ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}������a1=3��ͨ��an��ǰn���Sn֮������2an=SnSn��1��n��2����
��1����֤ ![]() �ǵȲ����У����
�ǵȲ����У����
��2��������{an}��ͨ�ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���֪�ڽ� ![]() ����
���� ![]() �����ڽ�B=x����ABC�����Ϊy��
�����ڽ�B=x����ABC�����Ϊy��
��1������y=f��x���Ľ���ʽ�Ͷ�����
��2������BΪ��ֵʱ����ABC��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ![]() �DZ߳�Ϊ
�DZ߳�Ϊ![]() �������Σ�
�������Σ� ![]() ƽ��
ƽ��![]() ��
�� ![]() ƽ��
ƽ��![]() ��
�� ![]() .
.
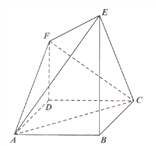
������֤�� ![]() ��
��
����������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() �ĵ�����
�ĵ�����![]() ��
��![]() ��
�� ![]() ��
��
��1����![]() �ļ�ֵ��
�ļ�ֵ��
��2����֤��������![]() ������
������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���״��ڵ�B������A����AB��10ǧ�ף��״���ÿСʱ4ǧ���ٶ����У�ͬʱ���Ҵ���B������ÿСʱ6ǧ���ٶ���ƫ��60��ķ���ʻȥ�����״���A��B֮�䣬�Ҽס�������������ʱ�����������е�ʱ����(����)

A. ![]() ���� B.
���� B. ![]() Сʱ C. 21.5���� D. 2.15����
Сʱ C. 21.5���� D. 2.15����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com