Question

【题目】已知函数

（1）若函数在定义域内单调递增，求的取值范围；

（2）若且关于的方程在上恰有两个不相等的实数根，求实数的取值范围．

Answer 1

【答案】（1）a的取值范围是（﹣∝，﹣1] （2）ln2﹣2＜b≤﹣

【解析】

本试题主要是考查了导数在研究函数中的 运用。求解函数的单调性，以及函数与方程根的综合运用。

（1）依题意函数在定义域内单调递增，即在时恒成立，即在恒成立.

则分离参数的思想得到在恒成立，即

（2）利用构造函数，利用函数的单调性，得到函数的极值，从而研究函数图像与坐标轴的交点问题，得到方程的解。

解： （1）

依题意在时恒成立，即在恒成立.

则在恒成立，即

当时，取最小值

∴的取值范围是………………6分

（2）

设则列表：

		极大值		极小值

∴极小值，极大值，又……8分

方程在[1，4]上恰有两个不相等的实数根.

则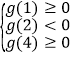， 得…………………12分