Question

【题目】已知函数f（x）＝lnx﹣ax，a∈R.

（1）若f（x）有两个零点，求a的取值范围；

（2）设函数g（x），证明：g（x）有极大值，且极大值小于.

Answer 1

【答案】（1）；（2）证明见解析.

【解析】

（1）由已知可得，，构造函数，转化为求解函数与的交点问题，结合函数的单调性即可求解.
（2）结合函数的导数与单调性的关系可证明的极值存在情况，然后结合函数的性质即可求解其范围.

（1）由f（x）＝lnx﹣ax＝0可得，a，

令h（x），则h′（x），

当x∈（0，e）时，h′（x）>0，h（x）单调递增，当x∈（e，+∞）时，h′（x）<0，h（x）单调递减，

∵h（e），

x→0，h（x）→﹣∞，x→+∞，h（x）→0，

∴a；

（2）∵g（x），

∴g′（x），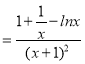

令I（x）＝1，则I（x）单调递减，

当x→0时，I（x）→+∞，当x→+∞时，I（x）→﹣∞，

∴I（x）一定存在变号的零点，g（x）存在极大值，

令I（x0）＝10，则g（x）在（0，x0）上单调递增，在（x0，+∞）上单调递减，

故极大值g（x0）a，

又∵I（3），

∴x0>3，又g（x0）在（0，+∞）上单调递减

∴g（x0）<