
【题目】如图,已知多面体![]() 中,
中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
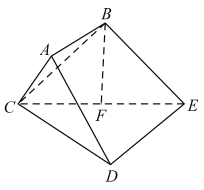
(1)求证:![]() 平面
平面![]() ;
;
(2)求多面体![]() 的体积;
的体积;
(3)求平面![]() 和平面
和平面![]() 所成的锐二面角的大小.
所成的锐二面角的大小.
【答案】(1)证明见解析;(2)![]() (3)
(3)![]() .
.
【解析】
(1)取![]() 中点
中点![]() ,根据已知,结合三角形中位线定理、平行四边形的判定定理和性质定理可以证明出
,根据已知,结合三角形中位线定理、平行四边形的判定定理和性质定理可以证明出![]() ,再根据线面垂直的性质、线面垂直的判定定理,结合等边三角形的性质进行证明即可;
,再根据线面垂直的性质、线面垂直的判定定理,结合等边三角形的性质进行证明即可;
(2)利用多面体![]() 的体积是两个三棱锥的体积之和,结合三棱锥的体积公式进行求解即可;
的体积是两个三棱锥的体积之和,结合三棱锥的体积公式进行求解即可;
(3)建立空间直角坐标系,利用空间向量夹角公式进行求解即可.
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,
,
因此有![]() 且
且![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,由已知可知:
,由已知可知:![]() ,
,
所以![]() 且
且![]() ,
,
因此![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,所以三角形
,所以三角形![]() 是等边三角形,而
是等边三角形,而![]() 是
是![]() 的中点,
的中点,
所以![]() ,而
,而![]() ,
,![]() 平面
平面![]() ,
,
因此![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ;
;
(2)因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
因此![]() ,因此有
,因此有![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
因此![]() ,
,
由![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
因此![]() ,
,
由(1)知:![]() ,所以
,所以![]() ,连接
,连接![]() ,
,
![]() ;
;
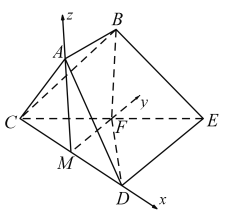
(3)建立如下图的所示的空间直角坐标系,![]()
![]() ,
,
设平面![]() 的法向量为:
的法向量为:![]() ,
,
![]() ,
,
因此有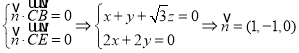 ,
,
平面![]() 的法向量为:
的法向量为:![]() ,
,
设平面![]() 和平面
和平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ,
,
则有 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】从集市上买回来的蔬菜仍存有残留农药,食用时需要清洗数次,统计表中的![]() 表示清洗的次数,
表示清洗的次数,![]() 表示清洗
表示清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量(单位:微克).
千克该蔬菜残留的农药量(单位:微克).
x | 1 | 2 | 3 | 4 | 5 |
y | 4.5 | 2.2 | 1.4 | 1.3 | 0.6 |
(1)在如图的坐标系中,描出散点图,并根据散点图判断,![]() 与
与![]() 哪一个适宜作为清洗
哪一个适宜作为清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量的回归方程类型;(给出判断即可,不必说明理由)
千克该蔬菜残留的农药量的回归方程类型;(给出判断即可,不必说明理由)

(2)根据判断及下面表格中的数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
表中![]() ,
,![]() .
.
|
|
|
|
|
| |
3 | 2 | 0.12 | 10 | 0.09 | -8.7 | 0.9 |
(3)对所求的回归方程进行残差分析.
附:①线性回归方程![]() 中系数计算公式分别为
中系数计算公式分别为 ,
,![]() ;
;
② ,
,![]() 说明模拟效果非常好;
说明模拟效果非常好;
③![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】原始的蚊香出现在宋代.根据宋代冒苏轼之名编写的《格物粗谈》记载:“端午时,贮浮萍,阴干,加雄黄,作纸缠香,烧之,能祛蚊虫.”如图,为某校数学兴趣小组用数学软件制作的“螺旋蚊香”,画法如下:在水平直线![]() 上取长度为1的线段
上取长度为1的线段![]() ,做一个等边三角形
,做一个等边三角形![]() ,然后以点
,然后以点![]() 为圆心,
为圆心,![]() 为半径逆时针画圆弧,交线段
为半径逆时针画圆弧,交线段![]() 的延长线于点
的延长线于点![]() ,再以点
,再以点![]() 为圆心,
为圆心,![]() 为半径逆时针画圆弧,交线段
为半径逆时针画圆弧,交线段![]() 的延长线于点
的延长线于点![]() ,以此类推,当得到的“螺旋蚊香”与直线
,以此类推,当得到的“螺旋蚊香”与直线![]() 恰有
恰有![]() 个交点时,“螺旋蚊香”的总长度的最小值为( )
个交点时,“螺旋蚊香”的总长度的最小值为( )
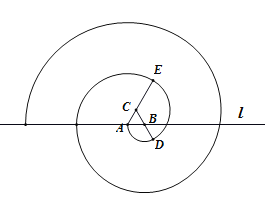
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,P为直线
中,P为直线![]() :
:![]() 上的动点,动点Q满足
上的动点,动点Q满足![]() ,且原点O在以
,且原点O在以![]() 为直径的圆上.记动点Q的轨迹为曲线C
为直径的圆上.记动点Q的轨迹为曲线C
(1)求曲线C的方程:
(2)过点![]() 的直线
的直线![]() 与曲线C交于A,B两点,点D(异于A,B)在C上,直线
与曲线C交于A,B两点,点D(异于A,B)在C上,直线![]() ,
,![]() 分别与x轴交于点M,N,且
分别与x轴交于点M,N,且![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国的西气东输工程把西部的资源优势变为经济优势,实现了气能源需求与供给的东西部衔接,工程建设也加快了西部及沿线地区的经济发展输气管道工程建设中,某段管道铺设要经过一处峡谷,峡谷内恰好有一处直角拐角,水平横向移动输气管经过此拐角,从宽为![]() 米峡谷拐入宽为
米峡谷拐入宽为![]() 米的峡谷.如图所示,位于峡谷悬崖壁上两点
米的峡谷.如图所示,位于峡谷悬崖壁上两点![]() 、
、![]() 的连线恰好经过拐角内侧顶点
的连线恰好经过拐角内侧顶点![]() (点
(点![]() 、
、![]() 、
、![]() 在同一水平面内),设
在同一水平面内),设![]() 与较宽侧峡谷悬崖壁所成角为
与较宽侧峡谷悬崖壁所成角为![]() ,则
,则![]() 的长为________(用
的长为________(用![]() 表示)米.要使输气管顺利通过拐角,其长度不能低于________米.
表示)米.要使输气管顺利通过拐角,其长度不能低于________米.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x-a|+|2x-1|(a∈R).
(1)当a=-1时,求f(x)≤2的解集;
(2)若f(x)≤|2x+1|的解集包含集合![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是无穷数列,若存在正整数k,使得对任意
是无穷数列,若存在正整数k,使得对任意![]() ,均有
,均有![]() ,则称
,则称![]() 是间隔递增数列,k是
是间隔递增数列,k是![]() 的间隔数,下列说法正确的是( )
的间隔数,下列说法正确的是( )
A.公比大于1的等比数列一定是间隔递增数列
B.已知![]() ,则
,则![]() 是间隔递增数列
是间隔递增数列
C.已知![]() ,则
,则![]() 是间隔递增数列且最小间隔数是2
是间隔递增数列且最小间隔数是2
D.已知![]() ,若
,若![]() 是间隔递增数列且最小间隔数是3,则
是间隔递增数列且最小间隔数是3,则![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com