
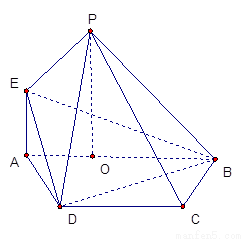
(本题12分)如图,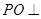 平面
平面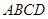 ,点
,点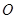 在
在 上,
上, ∥
∥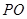 ,四边形
,四边形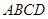 为直角梯形,
为直角梯形,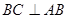 ,
,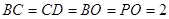 ,
,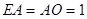
(1)求证: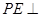 平面
平面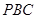 ;
;
(2)求二面角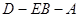 的余弦值;
的余弦值;
(3)直线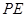 上是否存在点
上是否存在点 ,使
,使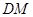 ∥平面
∥平面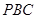 ,若存在,求出点
,若存在,求出点 ;若不存在,说明理由。
;若不存在,说明理由。
(1)只需证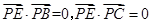 ;(2)
;(2)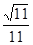 ;(3)存在M即为点E。
;(3)存在M即为点E。
【解析】
试题分析:四边形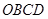 为正方形,所以
为正方形,所以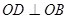 ,以OD为 x轴,OB为y轴,OP为z轴建立空间直角坐标系 …1分
,以OD为 x轴,OB为y轴,OP为z轴建立空间直角坐标系 …1分
(1)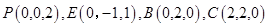 ,所以
,所以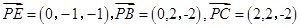 ,因为
,因为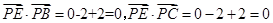 ,所以
,所以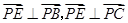 ,所以
,所以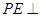 平面
平面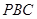 …………4分
…………4分
(2)平面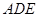 的法向量为
的法向量为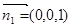 ,平面
,平面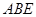 的法向量为
的法向量为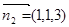
解得二面角的余弦值为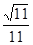 ……8分
……8分
(3)设 =
=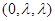 ,则
,则
由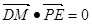 ,解得
,解得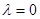 ,存在M即为点E ……12分
,存在M即为点E ……12分
考点:线面垂直的判定定理;二面角;线面平行的判定定理。
点评:证明线面垂直的常用方法:
①线线垂直Þ线面垂直
 若一条直线垂直平面内两条相交直线,则这条直线垂直这个平面。
若一条直线垂直平面内两条相交直线,则这条直线垂直这个平面。
即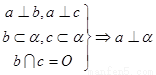
②面面垂直Þ线面垂直
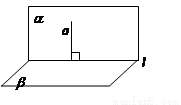 两平面垂直,其中一个平面内的一条直线垂直于它们的交线,则这条直线垂直于另一个平面。
两平面垂直,其中一个平面内的一条直线垂直于它们的交线,则这条直线垂直于另一个平面。
即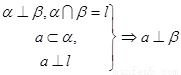
 ③两平面平行,有一条直线垂直于垂直于其中一个平面,则这条直线垂直于另一个平面。
③两平面平行,有一条直线垂直于垂直于其中一个平面,则这条直线垂直于另一个平面。
即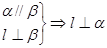
④两直线平行,其中一条直线垂直于这个平面,则另一条直线也垂直于这个平面。
 即
即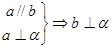
⑤向量法。


科目:高中数学 来源:2014届浙江省高二9月质量检测文科数学试卷(解析版) 题型:解答题
(本题12分)如图,在侧棱锥垂直底面的四棱锥ABCD-A1B1C1D1中,AD∥BC,
AD⊥AB,AB= 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
与直线AA1的交点。
(1)证明:(i)EF∥A1D1;
(ii)BA1⊥平面B1C1EF;
(2)求BC1与平面B1C1EF所成的角的正弦值。

查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高三全真模拟考试数学文卷 题型:解答题
((本题12分)如图所示,在直四棱柱 中,
中,  ,点
,点 是棱
是棱 上一点
上一点
(1)求证: 面
面 ;
;
(2)求证: ;
;

查看答案和解析>>
科目:高中数学 来源:2011-2012年山东省济宁市高二上学期期中考试文科数学 题型:解答题
(本题12分)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,M为线段AB的中点,将△ACD沿 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求二面角A-CD-M的余弦值.
查看答案和解析>>
科目:高中数学 来源:2013届四川省巴中市四县中高二上学期期末考试理科数学 题型:解答题
((本题12分)如图2,在棱长为1的正方体ABCD—A1B1C1D1中,点E、F、G分别是DD1、BD、BB1的中点。
(Ⅰ)求直线EF与直线CG所成角的余弦值;
(Ⅱ)求直线C1C与平面GFC所成角的正弦值;
(Ⅲ)求二面角E—FC—B的余弦值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com