
【题目】抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,若
,若![]() 为抛物线上第一象限的一动点,过
为抛物线上第一象限的一动点,过![]() 作
作![]() 的垂线交准线
的垂线交准线![]() 于点
于点![]() ,交抛物线于
,交抛物线于![]() 两点.
两点.
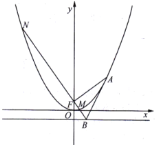
(Ⅰ)求证:直线![]() 与抛物线相切;
与抛物线相切;
(Ⅱ)若点![]() 满足
满足![]() ,求此时点
,求此时点![]() 的坐标.
的坐标.
【答案】(I)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)设![]() ,由此可得直线
,由此可得直线![]() 的斜率,进而得到直线
的斜率,进而得到直线![]() 的斜率,由此得到
的斜率,由此得到![]() 的方程为
的方程为![]() ,令
,令![]() 可得点
可得点![]() 的坐标,于是可得直线
的坐标,于是可得直线![]() 的斜率.然后再由导数的几何意义得到在点A处的切线的斜率,比较后可得结论.(Ⅱ)由(Ⅰ)知
的斜率.然后再由导数的几何意义得到在点A处的切线的斜率,比较后可得结论.(Ⅱ)由(Ⅰ)知![]() ,直线
,直线![]() 的方程为
的方程为![]() ,将直线方程与椭圆方程联立消元后得到二次方程,结合根与系数的关系及
,将直线方程与椭圆方程联立消元后得到二次方程,结合根与系数的关系及![]() 可求得点A的坐标.
可求得点A的坐标.
(Ⅰ)由题意得焦点![]() .设
.设![]() ,
,
∴直线![]() 的斜率为
的斜率为![]() ,
,
由已知直线![]() 斜率存在,且直线
斜率存在,且直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴直线![]() 的斜率为
的斜率为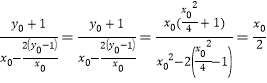 .
.
由![]() 得
得![]() ,
,
∴![]() ,即抛物线在点A处的切线的斜率为
,即抛物线在点A处的切线的斜率为![]() ,
,
∴直线![]() 与抛物线相切.
与抛物线相切.
(Ⅱ)由(Ⅰ)知![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
由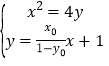 消去
消去![]() 整理得
整理得![]() ,
,
设![]() ,
,
则![]() .
.
由题意得直线![]() 的斜率为
的斜率为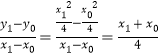 ,
,
直线![]() 的斜率为
的斜率为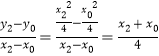 ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得![]() ,
,
解得![]() 或
或![]() .
.
∵![]() ,
,
∴![]() ,
,
又![]() ,且
,且![]() ,
,
∴存在![]() ,使得
,使得![]() .
.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,其中
,其中![]() ,则下列判断正确的是__________.(写出所有正确结论的序号)
,则下列判断正确的是__________.(写出所有正确结论的序号)
①![]() 关于点
关于点![]() 成中心对称;
成中心对称;
②![]() 在
在![]() 上单调递增;
上单调递增;
③存在![]() ,使
,使![]() ;
;
④若![]() 有零点,则
有零点,则![]() ;
;
⑤![]() 的解集可能为
的解集可能为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的方程为
的方程为![]() .
.
(1)以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,求曲线
轴的正半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,直线![]() 的极坐标方程为
的极坐标方程为![]() ,设曲线
,设曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,曲线
,曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com