
在锐角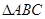 中,
中,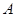 、
、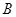 、
、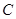 所对的边分别为
所对的边分别为 、
、 、
、 .已知向量
.已知向量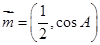 ,
,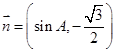 ,且
,且 .
.
(1)求角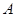 的大小;
的大小;
(2)若 ,
,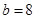 ,求
,求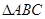 的面积.
的面积.
(1)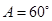 ;(2)
;(2)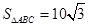 .
.
解析试题分析:(1)先根据平面向量垂直的等价条件得到等式 ,再利用弦化切的思想求出
,再利用弦化切的思想求出 的值,最终在求出角
的值,最终在求出角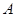 的值;(2)解法一:在角
的值;(2)解法一:在角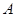 的大小确定的前提下,利用正弦定理与同角三角函数之间的关系求出
的大小确定的前提下,利用正弦定理与同角三角函数之间的关系求出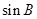 和
和 ,并利用
,并利用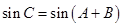 结合和角公式求出
结合和角公式求出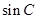 的值,最后利用面积公式
的值,最后利用面积公式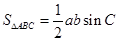 求出
求出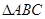 的面积;解法二:利用余弦定理求出
的面积;解法二:利用余弦定理求出 的值,并对
的值,并对 的值进行检验,然后面积公式
的值进行检验,然后面积公式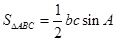 求出
求出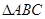 的面积.
的面积.
试题解析:(1)因为 ,所以
,所以 ,则
,则 , 4分
, 4分
因为 ,所以
,所以 ,则
,则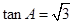 ,所以
,所以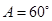 7分
7分
(2)解法一:由正弦定理得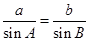 ,又
,又 ,
,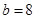 ,
,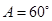 ,
,
则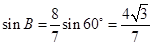 ,因为
,因为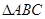 为锐角三角形,所以
为锐角三角形,所以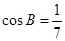 , 9分
, 9分
因为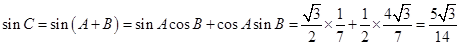 , 12分
, 12分
所以 14分
14分
解法二:因为 ,
,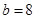 ,
,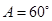 ,
,
所以由余弦定理可知,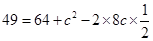 ,即
,即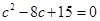 ,解得
,解得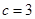 或
或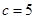 ,
,
当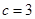 时,
时,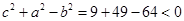 ,所以
,所以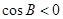 ,不合乎题意;
,不合乎题意;
当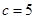 时,
时, ,所以
,所以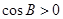 ,合乎题意;
,合乎题意;
所以 14分
14分
考点:正弦定理、余弦定理、同角三角函数的关系、两角和的正弦函数、三角形的面积公式


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com