
在△ABC中,内角A,B,C的对边分别为a,b,c.已知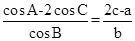 .
.
(Ⅰ)求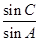 的值;
的值;
(Ⅱ)若cosB= ,
,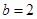 ,求
,求 的面积.
的面积.
(Ⅰ)2.(Ⅱ)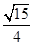
解析试题分析:(Ⅰ)本小题首先根据条件可知需要边角互化,于是考虑用正弦定理得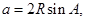
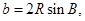
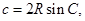 代入到条件中可得到三角之间的关系式,通过三角恒等变换可解得
代入到条件中可得到三角之间的关系式,通过三角恒等变换可解得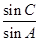 =2;(Ⅱ)根据(Ⅰ)知:
=2;(Ⅱ)根据(Ⅰ)知: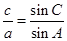 =2,即c=2a,经分析可发现具备余弦定理的条件,于是做余弦定理
=2,即c=2a,经分析可发现具备余弦定理的条件,于是做余弦定理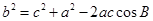 先求得
先求得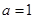 ,进而求得
,进而求得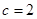 ,再求出夹角的正弦,最后利用面积公式
,再求出夹角的正弦,最后利用面积公式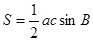 可求得三角形的面积.
可求得三角形的面积.
试题解析:(Ⅰ)由正弦定理得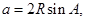
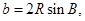
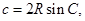
所以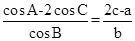 =
=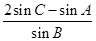 ,
,
即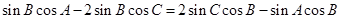 ,
,
即有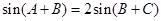 ,
,
即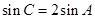 ,
,
所以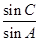 ="2." 6分
="2." 6分
(Ⅱ)由(Ⅰ)知: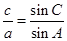 =2,即c=2a,
=2,即c=2a,
又因为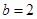 ,
,
所以由余弦定理得: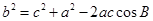 ,
,
即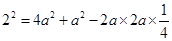 ,
,
解得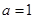 ,所以c=2,
,所以c=2,
又因为cosB= ,所以sinB=
,所以sinB=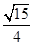 ,
,
故 的面积为
的面积为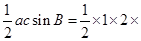
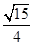 =
=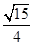 . 12分
. 12分
考点:1.正弦定理;2.余弦定理;3.三角形面积公式.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
如图,甲船以每小时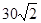 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,当甲船航行
海里,当甲船航行 分钟到达
分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距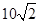 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com