
【题目】如图所示,四棱锥![]() 中,四边形
中,四边形![]() 是直角梯形,
是直角梯形, ![]() 底面
底面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 点在
点在![]() 上,且
上,且![]() .
.
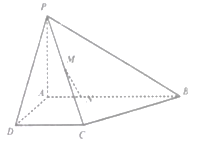
(1)证明: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)见解析;(II)![]() ,
,
【解析】试题分析:(1)要证MN∥平面PAD,只需在面PAD内找到一条直线和MN平行即可,而根据条件,易作辅助线过M作ME∥CD交PD于E,连接AE,下证MN∥AE;
(2)求直线MN与平面PCB所成的角,关键找直线MN在平面PCB内的射影,而根据条件,易作辅助线过N点作NQ∥AP交BP于点Q,NF⊥CB交CB于点F,连接QF,过N点作NH⊥QF交QF于H,连接MH,下证NH⊥平面PBC,∴∠NMH为直线MN与平面PCB所成的角.解△MNH即可.
试题解析:
(1)过点![]() 作
作![]() 交
交![]() 于
于![]() 点,连结
点,连结![]() ,
,
![]() , 又
, 又![]()
![]() 为平行四边形,
为平行四边形, ![]() 平面
平面![]() .
.
(2)过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,
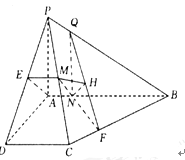
连结![]() ,过
,过![]() 点作
点作![]() 于
于![]() ,连结
,连结![]()
易知![]() 面
面![]() 而
而![]() 面
面![]() ,
,![]()
而![]() 面
面![]() ,
, ![]() 为直线
为直线![]() 与平面
与平面![]() 所成角,
所成角,
![]() 通过计算可得
通过计算可得![]() ,
,
 ,
,
![]() ,
,
![]() 直线
直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.


科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该定价按事先拟定的价格进行试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?
附:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网的发展,移动支付(又称手机支付)越来越普通,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有![]() 个人.把这
个人.把这![]() 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
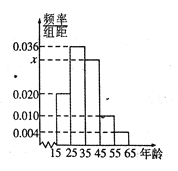
(1)求![]() 和
和![]() 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业实行裁员增效,已知现有员工![]() 人,每人每年可创纯收益(已扣工资等)1万元,据评估,在生产条件不变的情况下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人每位0.4万元的生活费,并且企业正常运转所需人数不得少于现有员工的
人,每人每年可创纯收益(已扣工资等)1万元,据评估,在生产条件不变的情况下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人每位0.4万元的生活费,并且企业正常运转所需人数不得少于现有员工的![]() ,设该企业裁员
,设该企业裁员![]() 人后,年纯收益为
人后,年纯收益为![]() 万元.
万元.
(1)写出![]() 关于
关于![]() 的函数关系式,并指出
的函数关系式,并指出![]() 的取值范围;
的取值范围;
(2)当![]() 时,该企业应裁员多少人,才能获得最大的经济效益(注:在保证能取得最大的经济效益的情况下,能少裁员,应尽量少裁员)?
时,该企业应裁员多少人,才能获得最大的经济效益(注:在保证能取得最大的经济效益的情况下,能少裁员,应尽量少裁员)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作一直线与抛物线
作一直线与抛物线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() 的距离最小的点,直线
的距离最小的点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.

(Ⅰ)求点![]() 的坐标;
的坐标;
(Ⅱ)求证:直线![]() 平行于抛物线的对称轴.
平行于抛物线的对称轴.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器由于使用时间较长,生产的零件有一些会有缺损,按不同转速生产出来的零件有缺损的统计数据如表所示:

(1)作出散点图;
(2)如果![]() 与
与![]() 线性相关,求出回归直线方程.
线性相关,求出回归直线方程.
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么,机器的运转速度应控制在什么范围内?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为,
的斜率和截距的最小二乘估计分别为,
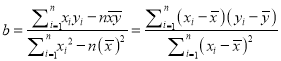 ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com