Question

【题目】已知点F2 ， P分别为双曲线 的右焦点与右支上的一点，O为坐标原点，若2 |，且 ，则该双曲线的离心率为（ ）
A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：设P（x，y），F1（﹣c，0），F2（c，0），

由题意可知：2 = + ，则M为线段PF2的中点，则M（ ， ），

则 =（c，0）， =（ ， ），

则 = ×c= 解得：x=2c，

由丨 丨=丨 丨=c，即 =c，解得：y= c，

则P（2c， c），由双曲线的定义可知：丨PF1丨﹣丨PF2丨=2a，

即 ﹣ =2a，a=（ ﹣1）c，

由双曲线的离心率e= = ，

∴该双曲线的离心率 ，

故选D．

方法二：由题意可知：2 = + ，则M为线段PF2的中点，

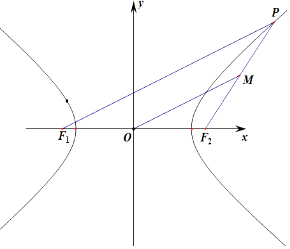
则OM为△F2F1P的中位线，

=﹣ =﹣丨 丨丨 丨cos∠OF2M= ，

由丨 丨=丨 丨=c，则cos∠OF2M=﹣ ，

由正弦定理可知：丨OM丨2=丨 丨2+丨 丨2﹣2丨 丨丨 丨cos∠OF2M=3c2，

则丨OM丨= c，则丨PF1丨=2 ，丨PF2丨=丨MF2丨=2c，

由双曲线的定义丨PF1丨﹣丨PF2丨=2a，a=（ ﹣1）c，

由双曲线的离心率e= = ，

∴该双曲线的离心率 ，

故选D．