
【题目】已知椭圆![]() 的中心在原点,焦点
的中心在原点,焦点![]() 、
、![]() 在
在![]() 轴上,离心率为
轴上,离心率为![]() ,在椭圆
,在椭圆![]() 上有一动点
上有一动点![]() 与
与![]() 、
、![]() 的距离之和为4,
的距离之和为4,
(Ⅰ) 求椭圆E的方程;
(Ⅱ) 过![]() 、
、![]() 作一个平行四边形,使顶点
作一个平行四边形,使顶点![]() 、
、![]() 、
、![]() 、
、![]() 都在椭圆
都在椭圆![]() 上,如图所示.判断四边形
上,如图所示.判断四边形![]() 能否为菱形,并说明理由.
能否为菱形,并说明理由.

【答案】(1) ![]() (2)
(2) ![]() 不能是菱形
不能是菱形
【解析】试题分析:(1)由椭圆离心率为![]() ,在椭圆E上有一动点A与F1、F2的距离之和为4,列出方程组,求出a=2,b=
,在椭圆E上有一动点A与F1、F2的距离之和为4,列出方程组,求出a=2,b=![]() ,由此能求出椭圆E的方程.(2)由F1(﹣1,0),令直线AB的方程为x=my﹣1,联立方程组
,由此能求出椭圆E的方程.(2)由F1(﹣1,0),令直线AB的方程为x=my﹣1,联立方程组![]() ,得(3m2+4)y2﹣6my﹣9=0,由此利用韦达定理、直线垂直的性质,结合已知条件能求出四边形ABCD不能是菱形.
,得(3m2+4)y2﹣6my﹣9=0,由此利用韦达定理、直线垂直的性质,结合已知条件能求出四边形ABCD不能是菱形.
解析:
(Ⅰ)由条件得![]() 所以
所以![]()
∴椭圆E的方程是![]()
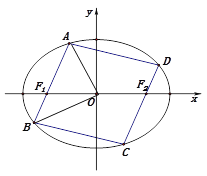
(Ⅱ)因为![]() ,如图,直线
,如图,直线![]() 不能平行于
不能平行于![]() 轴,所以令直线
轴,所以令直线![]() 的方程
的方程
为![]() ,
, ![]() ,
,
联立方程, ![]() ,
,
得![]() ,
,
∴![]() ,
, ![]() .
.
若![]() 是菱形,则
是菱形,则![]() ,
,
即![]() ,
,
于是有![]() ,
,
又![]()
![]() ,
,
所以有![]() ,
,
得到![]() ,
,
显然这个方程没有实数解,故![]() 不能是菱形.
不能是菱形.


科目:高中数学 来源: 题型:
【题目】三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=![]() ,AB=
,AB=![]() ,AC=2,A1C1=1,
,AC=2,A1C1=1,![]() .
.
(1)证明:BC![]() A1D;
A1D;
(2)求二面角A-CC1-B的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的命题有__________.
①回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ,且至少过一个样本点;
,且至少过一个样本点;
②将一组数据的每个数据都加一个相同的常数后,方差不变;
③用相关指数![]() 来刻面回归效果;表示预报变量对解释变量变化的贡献率,越接近于1,说明模型的拟合效果越好;
来刻面回归效果;表示预报变量对解释变量变化的贡献率,越接近于1,说明模型的拟合效果越好;
④若分类变量![]() 和
和![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 越大,则“
越大,则“![]() 与
与![]() 相关”的可信程度越小;
相关”的可信程度越小;
⑤.对于自变量![]() 和因变量
和因变量![]() ,当
,当![]() 取值一定时,
取值一定时, ![]() 的取值具有一定的随机性,
的取值具有一定的随机性, ![]() ,
, ![]() 间的这种非确定关系叫做函数关系;
间的这种非确定关系叫做函数关系;
⑥.残差图中残差点比较均匀的地落在水平的带状区域中,说明选用的模型比较合适;
⑦.两个模型中残差平方和越小的模型拟合的效果越好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次考试中,五名学生的数学、物理成绩如下表
学生 |
|
|
|
|
|
数学 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
(1)要在这五名学生中选2名参加一项活动,求选中的同学中至少有一人的物理成绩高于90分的概率.
(2)求出这些数据的线性回归直线方程.
参考公式回归直线的方程是: ![]() ,
,
其中对应的回归估计值.  ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的方程为y=3+ ![]() .
.
(1)写出曲线C的一个参数方程;
(2)在曲线C上取一点P,过点P作x轴,y轴的垂线,垂足分别为A,B,求矩形OAPB的周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,在点
,在点![]() 处的切线方程为
处的切线方程为![]()
(1)求函数![]() 的解析式;
的解析式;
(2)若过点![]() ),可作曲线
),可作曲线![]() 的三条切线,求实数
的三条切线,求实数![]() 的取值范围;
的取值范围;
(3)若对于区间![]() 上任意两个自变量的值
上任意两个自变量的值![]() ,都有
,都有![]() ,求实数
,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
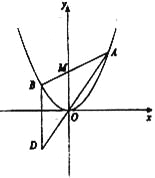
【题目】如图所示,已知抛物线![]() ,过点
,过点![]() 任作一直线与
任作一直线与![]() 相交于
相交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 相交于点
相交于点![]() 为坐标原点).
为坐标原点).
(1)证明: 动点![]() 在定直线上;
在定直线上;
(2)作![]() 的任意一条切线
的任意一条切线![]() (不含
(不含![]() 轴), 与直线
轴), 与直线![]() 相交于点
相交于点![]() 与(1)中的定直线相交于点
与(1)中的定直线相交于点![]() .
.
证明: ![]() 为定值, 并求此定值.
为定值, 并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线G:x2=2py(p>0),直线y=k(x﹣1)+2与抛物线G相交A(x1 , y1),B(x2 , y2)(x1<x2),过A,B点分别作抛物线G的切线L1 , L2 , 两切线L1 , L2相交H(x,y),
(1)若k=1,有 L1⊥L2 , 求抛物线G的方程;
(2)若p=2,△ABH的面积为S1 , 直线AB与抛物线G围成封闭图形的面积为S2 , 证明: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com