【题目】在矩形ABCD中，AB=1，AD=2，动点P在以C为圆心且与BD相切的圆上，则
的最大值为（ ）
A. 
B. 
C. -2 D. 0
第1卷单元月考期中期末系列答案科目：高中数学 来源： 题型：
【题目】某车间为了规定工时定额，需确定加工零件所花费的时间，为此做了4次试验，得到的数据如下：
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
若加工时间
与零件个数
之间有较好的相关关系．
（1）求加工时间与零件个数的线性回归方程
．
（2）试预报加工10个零件需要的时间．
附录：参考公式：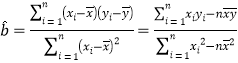
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在如图所示的几何体中，正方形
所在的平面与正三角形
所在的平面互相垂直， 
，且
， 
是
的中点．
（1）求证： 
平面
；
（2）求面
与面
所成锐二面角的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】探究函数
的最小值，并确定取得最小值时x的值.列表如下：
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
请观察表中y值随x值变化的特点，完成以下的问题.
函数
在区间（0，2）上递减；
函数
在区间 上递增.
当
时， 
.
证明：函数
在区间（0，2）递减.
思考：函数
时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
是定义在R上的函数，对任意实数x，有f（1﹣x）=x2﹣3x+3．
（1）求函数的解析式；
（2）若函数在g（x）=f（x）﹣（1+2m）x+1（m∈R）在
上的最小值为﹣2，求m的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的前n项和为Sn ， 数列{ 
}的公差为1的等差数列，且a2=3，a3=5．
（1）求数列{an}的通项公式；
（2）设bn=an3n ， 求数列{bn}的前n项和Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的中心在原点，焦点
、
在
轴上，离心率为
，在椭圆
上有一动点
与
、
的距离之和为4，
(Ⅰ) 求椭圆E的方程；
(Ⅱ) 过
、
作一个平行四边形，使顶点
、
、
、
都在椭圆
上，如图所示.判断四边形
能否为菱形，并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆心在
轴上的圆
与直线
切于点
.
（1）求圆
的标准方程；
（2）已知
，经过原点，且斜率为正数的直线
与圆
交于
两点.
（ⅰ）求证： 
为定值；
（ⅱ）求
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
