
【题目】
已知函数![]() ,其中
,其中![]() 是常数.
是常数.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 在
在![]() 上有两个不相等的实数根,求
上有两个不相等的实数根,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)当a=1时,f(1)=e,f′(1)=4e,由点斜式可求得y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ) 令f′(x)=ex[x2+(a+2)x)]=0,可解得x=﹣(a+2)或x=0,对﹣(a+2)与0的大小关系分类讨论,可求得关于x的方程f(x)=k在[0,+∞)上有两个不相等的实数根的k的取值范围.
解:(Ⅰ)由![]() 可得
可得
![]() .
.
当![]() 时,
时,![]() ,
,![]() .
.
所以 曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]()
(Ⅱ) 令![]() ,
,
解得![]() 或
或![]()
当![]() ,即
,即![]() 时,在区间
时,在区间![]() 上,
上,![]() ,所以
,所以![]() 是
是![]() 上的增函数.
上的增函数.
所以 方程![]() 在
在![]() 上不可能有两个不相等的实数根.
上不可能有两个不相等的实数根.
当![]() ,即
,即![]() 时,
时,![]() 随
随![]() 的变化情况如下表
的变化情况如下表
|
|
|
|
|
|
|
|
|
|
|
| ↘ |
| ↗ |
由上表可知函数![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
因为 函数![]() 是
是![]() 上的减函数,是
上的减函数,是![]() 上的增函数,
上的增函数,
且当![]() 时,有
时,有![]()
![]() .
.
所以 要使方程![]() 在
在![]() 上有两个不相等的实数根,
上有两个不相等的实数根,![]() 的取值范围必须是
的取值范围必须是
![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 在
在![]() 上有最大值1,设
上有最大值1,设![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 有三个不同的零点,求实数
有三个不同的零点,求实数![]() 的取值范围(
的取值范围(![]() 为自然对数的底数).
为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,则直线
,则直线![]() 称为抛物线
称为抛物线![]() 的伴随直线.
的伴随直线.
(1)求抛物线![]() 的伴随直线的表达式;
的伴随直线的表达式;
(2)已知抛物线![]() 的伴随直线为
的伴随直线为![]() ,且该抛物线与
,且该抛物线与![]() 轴有两个不同的公共点,求
轴有两个不同的公共点,求![]() 的取值范围.
的取值范围.
(3)已知![]() ,若抛物线
,若抛物线![]() 的伴随直线为
的伴随直线为![]() ,且该抛物线与线段
,且该抛物线与线段![]() 恰有1个公共点,求
恰有1个公共点,求![]() 的取值范围(直接写出答案即可)
的取值范围(直接写出答案即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为双曲线
为双曲线![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,并在
轴的直线,并在![]() 轴上方交双曲线于点
轴上方交双曲线于点![]() ,且
,且![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 上一点
上一点![]() 作两条渐近线的垂线,垂足分别是
作两条渐近线的垂线,垂足分别是![]() 和
和![]() ,试求
,试求![]() 的值;
的值;
(3)过圆![]() 上任意一点
上任意一点![]() 作切线
作切线![]() 交双曲线
交双曲线![]() 于
于![]() 两个不同点,
两个不同点,![]() 中点为
中点为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一年级6个班级去苏州、黄山、厦门三个地方修学旅行,每个城市至少有一个班前去,其中1班和2班不能去同一个地方,则共有_________种不同分配方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|

(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
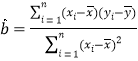
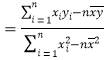 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据不完全统计,某厂的生产原料耗费![]() (单位:百万元)与销售额
(单位:百万元)与销售额![]() (单位:百万元)如下:
(单位:百万元)如下:
| 2 | 4 | 6 | 8 |
| 30 | 40 | 50 | 70 |
变量![]() 、
、![]() 为线性相关关系.
为线性相关关系.
(1)求线性回归方程必过的点;
(2)求线性回归方程;
(3)若实际销售额要求不少于![]() 百万元,则原材料耗费至少要多少百万元。
百万元,则原材料耗费至少要多少百万元。
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E、F分别是PC、AD中点,
(1)求证:DE//平面PFB;
(2)求PB与面PCD所成角的正切值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com