【题目】已知椭圆
的离心率为
，左顶点为
，过原点且斜率不为0的直线与椭圆交于
两点，其中点
在第二象限，过点
作
轴的垂线交
于点
．
⑴求椭圆的标准方程；
⑵当直线
的斜率为
时，求
的面积；
⑶试比较
与
大小．
【答案】⑴
⑵
⑶见解析
【解析】试题分析：（1）利用离心率、左顶点坐标求解即可；（2）根据直线过原点且斜率为
写出直线方程，联立直线和椭圆方程，求出
，再写出直线
的方程，求出点
的坐标，利用三角形的面积公式进行求解；（3）设直线
的方程为
， 
，与椭圆方程联立，得到关于
的一元二次方程，利用根与系数的关系、弦长公式及椭圆的对称性进行求解.
试题解析：⑴因为左顶点为
，所以
因为椭圆的离心率为
，所以
，解得
又因为
，所以
故所求椭圆的标准方程为
⑵因为直线
过原点，且斜率为
所以直线
的方程为
代入椭圆方程
解得
因为
，所以直线
的方程为
从而有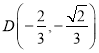
故
的面积等于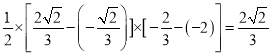
⑶方法一：
设直线
的方程为
， 
代入椭圆方程得
设
，则有
，解得
从而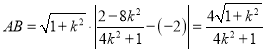
由椭圆对称性可得
所以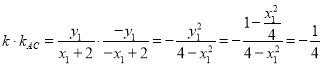
于是
故
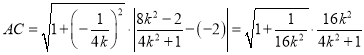
从而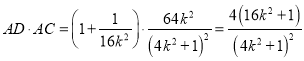
所以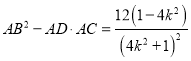
因为点
在第二象限，所以
，于是有
方法二：
设点
，则点
因为
，所以直线
的方程为
所以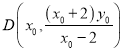
从而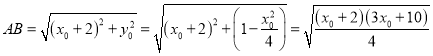
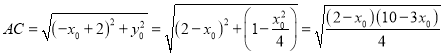
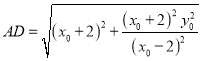
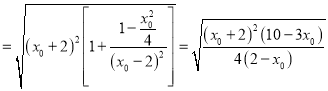
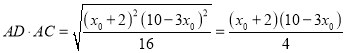
从而有
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生，按其数学成绩（均为整数）分成六组
， 
，…， 
后得到如下部分频率分布直方图，观察图中的信息，回答下列问题：
（1）补全频率分布直方图；
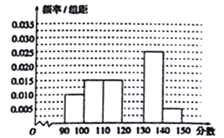
（2）估计本次考试的数学平均成绩（同一组中的数据用该组区间的中点值作代表）；
（3）用分层抽样的方法在分数段为
的学生成绩中抽取一个容量为6的样本，再从这6个样本中任取2人成绩，求至多有1人成绩在分数段
内的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，在长方形
中，
为
的中点，
为线段
上一动点．现将
沿
折起，形成四棱锥
.
图1 图2 图3
（Ⅰ）若与
重合，且
(如图2).
(ⅰ)证明：
平面
；
(ⅱ)求二面角
的余弦值.
（Ⅱ）若不与重合，且平面
平面
(如图3)，设
，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从含有两件正品a,b和一件次品c的3件产品中每次任取一件，连续取两次，求取出的两件产品中，恰有一件是次品的概率。
（1）每次取出不放回；（2）每次取出放回；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P﹣A1B1C1D1 ， 下部的形状是正四棱柱ABCD﹣A1B1C1D1（如图所示），并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍．
（1）若AB=6m，PO1=2m,则仓库的容积是多少？
（2）若正四棱柱的侧棱长为6m,则当PO1为多少时，仓库的容积最大？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ax+bx（a＞0，b＞0，a≠1，b≠1）．
（1）设a=2,b= 
.
①求方程f（x）=2的根；
②若对于任意x∈R，不等式f（2x）≥mf（x）﹣6恒成立，求实数m的最大值；
（2）若0＜a＜1，b＞1，函数g（x）=f（x）﹣2有且只有1个零点，求ab的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，点列{An}、{Bn}分别在某锐角的两边上且|AnAn+1|=|An+1An+2|，An≠An+1 ， n∈N* ， |BnBn+1|=|Bn+1Bn+2|，Bn≠Bn+1 ， n∈N* ， （P≠Q表示点P与Q不重合）若dn=|AnBn|，Sn为△AnBnBn+1的面积，则（ ）
A.{Sn}是等差数列
B.{Sn2}是等差数列
C.{dn}是等差数列
D.{dn2}是等差数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
