
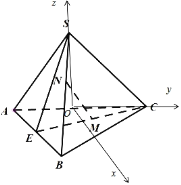
【题目】在三棱锥,![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
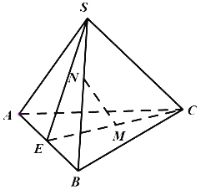
(1)证明:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置并给出证明,若不存在,说明理由;
的位置并给出证明,若不存在,说明理由;
(3)若![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析;(2)存在,点![]() 为
为![]() 上的靠近
上的靠近![]() 的四等分点;(3)
的四等分点;(3)![]() .
.
【解析】
(1)先证明![]() 平面
平面![]() ,再利用面面垂直的判定定理得到结论;
,再利用面面垂直的判定定理得到结论;
(2)取点![]() 为
为![]() 上的靠近
上的靠近![]() 的四等分点即
的四等分点即![]() ,
,![]() 平面
平面![]() ,利用面面平行,判断出线面平行,判断出结论成立;
,利用面面平行,判断出线面平行,判断出结论成立;
(3)根据题意,作![]() 于
于![]() ,过
,过![]() 作
作![]() 的平行线为
的平行线为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,平面
轴,建立空间直角坐标系,平面![]() 的法向量为
的法向量为![]() ,求出平面
,求出平面![]() 的法向量,利用夹角公式求出二面角的余弦值,求出角.
的法向量,利用夹角公式求出二面角的余弦值,求出角.
解:(1)由![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() ,由
,由![]() ,
,![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
故平面![]() 平面
平面![]() ;
;
(2)存在点![]() 为
为![]() 上的靠近
上的靠近![]() 的四等分点即
的四等分点即![]() ,
,![]() 平面
平面![]() ,
,
证明如下:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
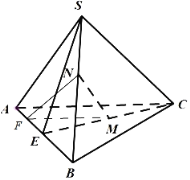
(3)作![]() 于
于![]() ,过
,过![]() 作
作![]() 的平行线为
的平行线为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
由![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故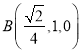 ,
,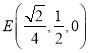 ,
,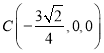 ,
,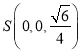 ,
,
![]() ,
,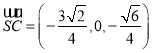 ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由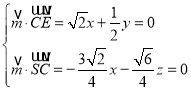 ,得
,得![]() ,
,
平面![]() 的法向量为
的法向量为![]() ,
,
由![]() ,因为二面角
,因为二面角![]() 为钝角,
为钝角,
故所求二面角为![]() .
.


科目:高中数学 来源: 题型:
【题目】![]() 年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的
年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的![]() 次线上测试成绩进行统计如图所示:
次线上测试成绩进行统计如图所示:
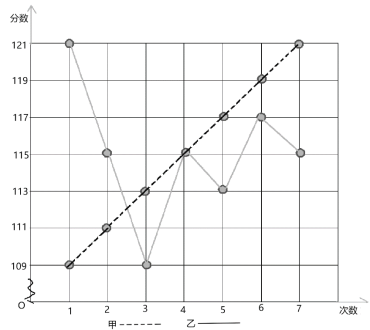
(1)请填写下表(要求写出计算过程)
平均数 | 方差 | |
甲 | ||
乙 |
(2)从下列三个不同的角度对这次方案选择的结果进行
①从平均数和方差相结合看(分析哪种方案的成绩更好);
②从折线图上两种方案的走势看(分析哪种方案更有潜力).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界第一产粮大国,我国粮食产量很高,整体很安全按照14亿人口计算,中国人均粮食产量约为950斤﹣比全球人均粮食产量高了约250斤.如图是中国国家统计局网站中2010﹣2019年,我国粮食产量(千万吨)与年末总人口(千万人)的条形图,根据如图可知在2010﹣2019年中( )
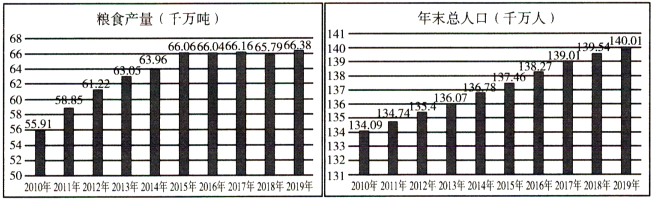
A.我国粮食年产量与年末总人口均逐年递增
B.2011年我国粮食年产量的年增长率最大
C.2015年﹣2019年我国粮食年产量相对稳定
D.2015年我国人均粮食年产量达到了最高峰
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①AB⊥BC,②FC与平面ABCD所成的角为![]() ,③∠ABC
,③∠ABC![]() .
.
如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,,PD的中点为F.
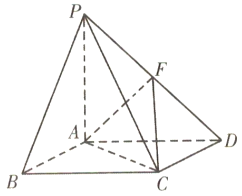
(1)在线段AB上是否存在一点G,使得AF![]() 平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
(2)若_______,求二面角F﹣AC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方、堑堵、阳马、鱉臑这些名词出自中国古代数学名著《九章算术商功》.其中阳马和鱉臑是我国古代对一些特殊锥体的称呼.取一长方,如图长方体ABCD﹣A1B1C1D1,按平面ABC1D1斜切一分为二,得到两个一模一样的三棱柱.称该三梭柱为堑堵,再沿堑堵的一顶点与相对的棱剖开,得四棱锥和三棱锥各一个,其中以矩形为底另有一棱与底面垂直的四梭锥D1﹣ABCD称为阳马,余下的三棱锥D1﹣BCC1是由四个直角三角形组成的四面体称为鱉臑.已知长方体ABCD﹣A1B1C1D1中,AB=5,BC=4,AA1=3,按以上操作得到阳马.则该阳马的最长棱长为_____.
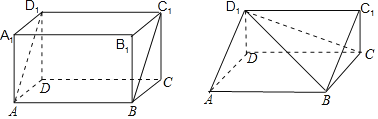
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为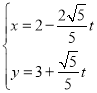 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 的参数方程与直线
的参数方程与直线![]() 的普通方程;
的普通方程;
(Ⅱ)设点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 和点
和点![]() 为直线
为直线![]() 上的点,且
上的点,且![]() .求
.求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】产量相同的机床一和机床二生产同一种零件,在一个小时内生产出的次品数分别记为![]() ,
,![]() ,它们的分布列分别如下:
,它们的分布列分别如下:
| 0 | 1 | 2 | 3 |
| 0.4 | 0.3 | 0.2 | 0.1 |
| 0 | 1 | 2 |
| 0.2 | 0.6 | 0.2 |
(1)哪台机床更好?请说明理由;
(2)记![]() 表示
表示![]() 台机床
台机床![]() 小时内共生产出的次品件数,求
小时内共生产出的次品件数,求![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com