
【题目】2018年辽宁省正式实施高考改革.新高考模式下,学生将根据自己的兴趣、爱好、学科特长和高校提供的“选考科目要求”进行选课.这样学生既能尊重自己爱好、特长做好生涯规划,又能发挥学科优势,进而在高考中获得更好的成绩和实现自己的理想.考改实施后,学生将在高二年级将面临着![]() 的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
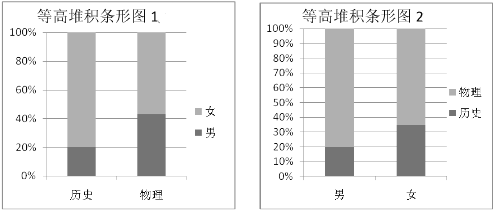
A.样本中的女生数量多于男生数量
B.样本中有学物理意愿的学生数量多于有学历史意愿的学生数量
C.样本中的男生偏爱物理
D.样本中的女生偏爱历史
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(1)求函数![]() 的最大值与最小值;
的最大值与最小值;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后,得到函数
个单位后,得到函数![]() 的图象;已知点
的图象;已知点![]() ,若函数
,若函数![]() 的图象上存在点
的图象上存在点![]() ,使得
,使得![]() ,求函数
,求函数![]() 图象的对称中心.
图象的对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,并且
,并且![]() ,
,![]() ,数列
,数列![]() 满足:
满足:![]() ,
,![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和公式
项和公式![]() ;
;
(2)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和公式
项和公式![]() ;
;
(3)记集合![]() ,若
,若![]() 的子集个数为16,求实数
的子集个数为16,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,点P为双曲线C右支上异于顶点的一点,
,点P为双曲线C右支上异于顶点的一点,![]() 的内切圆与x轴切于点
的内切圆与x轴切于点![]() ,且直线
,且直线![]() 经过线段
经过线段![]() 的中点且垂直于线段
的中点且垂直于线段![]() ,则双曲线C的方程为________________.
,则双曲线C的方程为________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了配合今年上海迪斯尼游园工作,某单位设计了统计人数的数学模型![]() :以
:以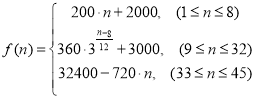 表示第
表示第![]() 个时刻进入园区的人数;以
个时刻进入园区的人数;以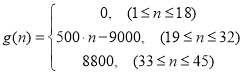 表示第
表示第![]() 个时刻离开园区的人数.设定以
个时刻离开园区的人数.设定以![]() 分钟为一个计算单位,上午
分钟为一个计算单位,上午![]() 点
点![]() 分作为第
分作为第![]() 个计算人数单位,即
个计算人数单位,即![]() ;
;![]() 点
点![]() 分作为第
分作为第![]() 个计算单位,即
个计算单位,即![]() ;依次类推,把一天内从上午
;依次类推,把一天内从上午![]() 点到晚上
点到晚上![]() 点
点![]() 分分成
分分成![]() 个计算单位(最后结果四舍五入,精确到整数).
个计算单位(最后结果四舍五入,精确到整数).
(1)试计算当天![]() 点至
点至![]() 点这一小时内,进入园区的游客人数
点这一小时内,进入园区的游客人数![]() 、离开园区的游客人数
、离开园区的游客人数![]() 各为多少?
各为多少?
(2)假设当日园区游客总人数达到或超过![]() 万时,园区将采取限流措施.该单位借助该数学模型知晓当天
万时,园区将采取限流措施.该单位借助该数学模型知晓当天![]() 点(即
点(即![]() )时,园区总人数会达到最高,请问当日是否要采取限流措施?说明理由.
)时,园区总人数会达到最高,请问当日是否要采取限流措施?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 是坐标轴上两点,动点
是坐标轴上两点,动点![]() 满足直线
满足直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() (其中
(其中![]() 为常数,且
为常数,且![]() ).记
).记![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)过点![]() 斜率为
斜率为![]() 的直线与曲线
的直线与曲线![]() 交于点
交于点![]() ,点
,点![]() 在曲线
在曲线![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的焦距为
)的焦距为![]() ,且右焦点F与短轴的两个端点组成一个正三角形.若直线l与椭圆C交于
,且右焦点F与短轴的两个端点组成一个正三角形.若直线l与椭圆C交于![]() 、
、![]() ,且在椭圆C上存在点M,使得:
,且在椭圆C上存在点M,使得:![]() (其中O为坐标原点),则称直线l具有性质H.
(其中O为坐标原点),则称直线l具有性质H.
(1)求椭圆C的方程;
(2)若直线l垂直于x轴,且具有性质H,求直线l的方程;
(3)求证:在椭圆C上不存在三个不同的点P、Q、R,使得直线![]() 、
、![]() 、
、![]() 都具有性质H.
都具有性质H.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)若![]() ,证明:函数
,证明:函数![]() 在区间
在区间![]() 上是单调增函数;
上是单调增函数;
(2)求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)若函数![]() 的图像过原点,且
的图像过原点,且![]() 的导数
的导数![]() ,当
,当![]() 时,函数
时,函数![]() 过点
过点![]() 的切线至少有2条,求实数
的切线至少有2条,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com