
【题目】已知四棱锥P-ABCD的三视图如下图所示,E是侧棱PC上的动点.
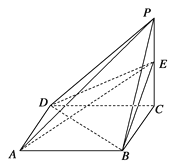

(1)求证:BD⊥AE
(2)若点E为PC的中点,求二面角D-AE-B的大小.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)要证明线线垂直,先证明线面垂直,所以观察几何体,先证明![]() 平面
平面![]() ,而要证明线面垂直,先证明线与平面内的两条相交直线垂直,即证明
,而要证明线面垂直,先证明线与平面内的两条相交直线垂直,即证明![]() ,
,![]() ;
;
(2)法一,几何法,观察![]() ,所以可选择在平面DAE内过点D作DF⊥AE于F,连结BF,∠DFB为二面角D-AE-B的平面角,或法二,采用空间向量的方法,以点C为原点,CD,CB,CP所在的直线分别为x,y,z轴建立空间直角坐标系,分别求两个平面的法向量,
,所以可选择在平面DAE内过点D作DF⊥AE于F,连结BF,∠DFB为二面角D-AE-B的平面角,或法二,采用空间向量的方法,以点C为原点,CD,CB,CP所在的直线分别为x,y,z轴建立空间直角坐标系,分别求两个平面的法向量,![]() 或
或![]() .
.
试题解析:(1)由三视图可知,四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC=2.
连结AC,∵ABCD是正方形, ∴BD⊥AC.
∵PC⊥底面ABCD,且BD平面ABCD, ∴BD⊥PC.
又∵AC∩PC=C,∴BD⊥平面PAC.
∵AE平面PAC. ∴BD⊥AE.
(2)解法1:在平面DAE内过点D作DF⊥AE于F,连结BF.
∵AD=AB=1,DE=BE=![]() ,AE=AE=
,AE=AE=![]() ,
,
∴Rt△ADE≌Rt△ABE,
从而△ADF≌△ABF,∴BF⊥AE.
∴∠DFB为二面角D-AE-B的平面角.
在Rt△ADE中,DF=![]() , ∴
, ∴![]() .
.
又BD=![]() ,在△DFB中,由余弦定理得
,在△DFB中,由余弦定理得
cos∠DFB=![]() ,
,
∴∠DFB=![]() ,即二面角D-AE-B的大小为
,即二面角D-AE-B的大小为![]()
解法2:如图,以点C为原点,CD,CB,CP所在的直线分别为x,y,z轴建立空间直角坐标系.则D(1,0,0),A(1,1,0),B(0,1,0),E(0,0,1),
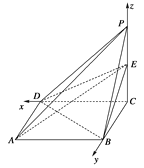
从而![]() =(0,1,0),
=(0,1,0),![]() =(-1,0,1),
=(-1,0,1),![]() =(1,0,0),
=(1,0,0),![]() =(0,-1,1).[Z#x设平面ADE和平面ABE的法向量分别为
=(0,-1,1).[Z#x设平面ADE和平面ABE的法向量分别为![]() ,
,![]()
由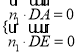
![]() ,取
,取![]()
由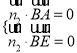
![]() ,取
,取![]()
设二面角D-AE-B的平面角为θ,则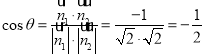 ,
,
∴θ=![]() ,即二面角D-AE-B的大小为
,即二面角D-AE-B的大小为![]()


科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵(qian du);阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖膈(bie nao)指四个面均为直角三角形的四面体.如图在堑堵![]() 中,
中,![]() ,
,![]() .给出下列四个结论:
.给出下列四个结论:
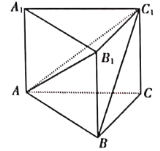
①四棱锥![]() 为阳马;
为阳马;
②直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ;
;
③当![]() 时,异面直线
时,异面直线![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]() ;
;
④当三棱锥![]() 体积最大时,四棱锥
体积最大时,四棱锥![]() 的外接球的表面积为
的外接球的表面积为![]() .
.
其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若一个函数存在极大值,且该极大值为负数,则称这个函数为“![]() 函数”.
函数”.
(1)判断函数![]() 是否为“
是否为“![]() 函数”,并说明理由;
函数”,并说明理由;
(2)若函数![]() 是“
是“![]() 函数”,求实数
函数”,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() ,
,![]() ,
,![]() 、
、![]() ,求证:当
,求证:当![]() ,且
,且![]() 时,函数
时,函数![]() 是“
是“![]() 函数”.
函数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是正方体
是正方体![]() 的棱
的棱![]() 的中点,下列命题中真命题是( )
的中点,下列命题中真命题是( )
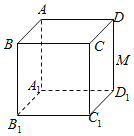
A.过![]() 点有且只有一条直线与直线
点有且只有一条直线与直线![]()
![]() 都相交
都相交
B.过![]() 点有且只有一条直线与直线
点有且只有一条直线与直线![]()
![]() 都垂直
都垂直
C.过![]() 点有且只有一个平面与直线
点有且只有一个平面与直线![]()
![]() 都相交
都相交
D.过![]() 点有且只有一个平面与直线
点有且只有一个平面与直线![]()
![]() 都平行
都平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com