
【题目】选修4-4:坐标系与参数方程
已知直线l过定点P(1,1),且倾斜角为 ![]() ,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程与直线l的参数方程;
(2)若直线l与曲线C相交于不同的两点A,B,求|AB|及|PA||PB|的值.
【答案】
(1)解:∵曲线C的极坐标方程为 ![]() ,
,
∴ρ2=2ρcosθ+3,
将ρ2=x2+y2,ρcosθ=x代入,得x2+y2=2x+3,即x2+y2﹣2x﹣3=0.
∵直线l过定点P(1,1),且倾斜角为 ![]() ,
,
则直线l的参数方程为 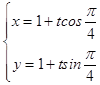 ,即
,即 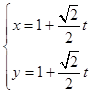 (t为参数)
(t为参数)
(2)解:将直线l的参数方程代入x2+y2﹣2x﹣3=0,得 ![]() ,
,
设方程两根分别为t1,t2,则 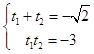 ,
,
∴AB的长|AB|=|t1﹣t2|= ![]() =
= ![]() =
= ![]() ,
,
|PA||PB|=|t1t2|=3
【解析】(1)曲线C的极坐标方程转为ρ2=2ρcosθ+3,将ρ2=x2+y2,ρcosθ=x代入,能求出曲线C的直角坐标方程;由直线l过定点P(1,1),且倾斜角为 ![]() ,能求出直线l的参数方程.(2)将直线l的参数方程代入x2+y2﹣2x﹣3=0,得
,能求出直线l的参数方程.(2)将直线l的参数方程代入x2+y2﹣2x﹣3=0,得 ![]() ,设方程两根分别为t1,t2,利用韦达定理及弦长公式能求出|AB|及|PA||PB|的值.
,设方程两根分别为t1,t2,利用韦达定理及弦长公式能求出|AB|及|PA||PB|的值.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期为4π,且对x∈R,有f(x)≤f(
)的最小正周期为4π,且对x∈R,有f(x)≤f( ![]() )成立,则关于函数f(x)的下列说法中正确的是( )
)成立,则关于函数f(x)的下列说法中正确的是( )
①φ= ![]()
②函数f(x)在区间[﹣π,π]上递减;
③把g(x)=sin ![]() 的图象向左平移
的图象向左平移 ![]() 得到f(x)的图象;
得到f(x)的图象;
④函数f(x+ ![]() )是偶函数.
)是偶函数.
A.①③
B.①②
C.②③④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() =1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2 , 过点A且斜率为
=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2 , 过点A且斜率为 ![]() 的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1 .
的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1 .
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点P且斜率大于 ![]() 的直线与椭圆交于M,N两点(|PM|>|PN|),若S△PAM:S△PBN=λ,求实数λ的取值范围.
的直线与椭圆交于M,N两点(|PM|>|PN|),若S△PAM:S△PBN=λ,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() 的两个焦点为
的两个焦点为 ![]() 的曲线C上.
的曲线C上.
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q(0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,a3=9,且an=an﹣1+λn﹣1(n≥2).
( I)求λ的值及数列{an}的通项公式;
( II)设 ![]() ,且数列{bn}的前n项和为Sn , 求S2n .
,且数列{bn}的前n项和为Sn , 求S2n .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,已知|AB|=|AC|=1,∠A=120°,E,F分别是AB,AC上的点,且 ![]() ,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则
,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则 ![]() 的最小值为 .
的最小值为 . 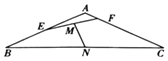
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
设函数f(x)=|x+ ![]() |+|x﹣2m|(m>0).
|+|x﹣2m|(m>0).
(1)求证:f(x)≥8恒成立;
(2)求使得不等式f(1)>10成立的实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过正方体ABCD﹣A1B1C1D1的顶点A1在空间作直线l,使l与直线AC和BC1所成的角都等于 ![]() ,则这样的直线l共可以作出( )
,则这样的直线l共可以作出( )
A.1条
B.2条
C.3条
D.4条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com