
已知二次函数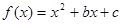 与
与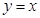 交于
交于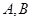 两点且
两点且 ,奇函数
,奇函数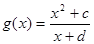 ,当
,当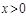 时,
时,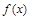 与
与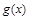 都在
都在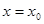 取到最小值.
取到最小值.
(1)求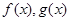 的解析式;
的解析式;
(2)若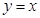 与
与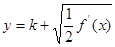 图象恰有两个不同的交点,求实数
图象恰有两个不同的交点,求实数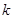 的取值范围.
的取值范围.
(1)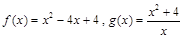 ;(2)
;(2)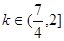 .
.
【解析】
试题分析:(1)由已知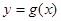 是奇函数,故
是奇函数,故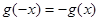 ,从而得
,从而得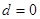 ,所以
,所以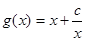 ,又当
,又当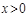 时,
时,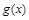 在
在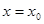 取到最小值,由均值不等式等号成立的条件可得
取到最小值,由均值不等式等号成立的条件可得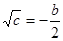 ,即
,即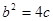 .再由已知
.再由已知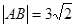 及弦长公式,得
及弦长公式,得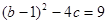 ,解方程组便得
,解方程组便得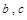 的值,从而得函数
的值,从而得函数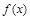 和
和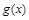 的解析式;(2)由已知,
的解析式;(2)由已知,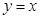 与
与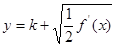 ,即
,即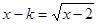 有两个不等的实根,将问题转化为方程
有两个不等的实根,将问题转化为方程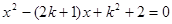
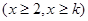 有两个不等的实根,即一元二次方程根的分布问题,列不等式组解决问题.
有两个不等的实根,即一元二次方程根的分布问题,列不等式组解决问题.
试题解析:(1)因为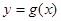 是奇函数,由
是奇函数,由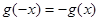 得
得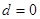 ,所以
,所以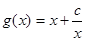 ,由于
,由于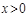 时,
时,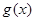 有最小值,所以
有最小值,所以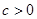 ,则
,则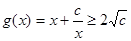 ,当且仅当:
,当且仅当: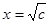 取到最小值,所以
取到最小值,所以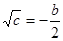 ,即
,即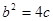 .
.
设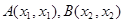 ,
,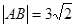 ,则
,则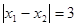 .由
.由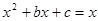 得:
得: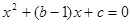 ,所以:
,所以: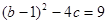 ,解得:
,解得: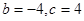 ,所以
,所以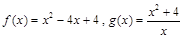 6分
6分
(2)因为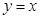 与
与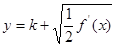 ,即
,即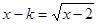 有两个不等的实根,也即方程
有两个不等的实根,也即方程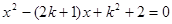
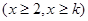 有两个不等的实根.
有两个不等的实根.
当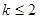 时,有
时,有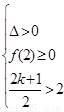 ,解得
,解得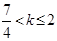 ;当
;当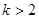 时,有
时,有 ,无解.
,无解.
综上所述,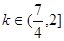 .
13分
.
13分
考点:1.函数的最值;2.函数的奇偶性;3.弦长公式;4.一元二次方程根的分布问题.


科目:高中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源:2014届安徽省六校教育研究会高三素质测试文科数学试卷(解析版) 题型:解答题
已知二次函数 与两坐标轴分别交于不同的三点A、B、C.
与两坐标轴分别交于不同的三点A、B、C.
(1)求实数t的取值范围;
(2)当 时,求经过A、B、C三点的圆F的方程;
时,求经过A、B、C三点的圆F的方程;
(3)过原点作两条相互垂直的直线分别交圆F于M、N、P、Q四点,求四边形 的面积的最大值。
的面积的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com