
【题目】如图,在几何体![]() 中,四边形
中,四边形![]() ,
,![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 的中点.
的中点.
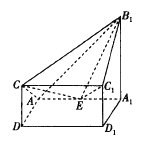
(1)证明:![]() ;
;
(2)设![]() 与
与![]() 的交点为
的交点为![]() ,试问:在线段
,试问:在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() .
.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】在信息时代的今天,随着手机的发展,“微信”越来越成为人们交流的一种方法,某机构对“使用微信交流”的态度进行调查,随机抽取了100人,他们年龄的频数分布及对“使用微信交流”赞成的人数如下表:(注:年龄单位:岁)
年龄 |
|
|
|
|
|
|
频数 | 10 | 30 | 30 | 20 | 5 | 5 |
赞成人数 | 9 | 25 | 24 | 9 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面的![]() 列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在![]() ,
,![]() 调查的人中各随机选取1人进行追踪调查,求选中的2人中赞成“使用微信交流”的人数恰好为1人的概率.
调查的人中各随机选取1人进行追踪调查,求选中的2人中赞成“使用微信交流”的人数恰好为1人的概率.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直角三角形ABC的三个顶点都在椭圆![]() 上,其中A(0,1)为直角顶点.若该三角形的面积的最大值为
上,其中A(0,1)为直角顶点.若该三角形的面积的最大值为![]() ,则实数a的值为_____.
,则实数a的值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.
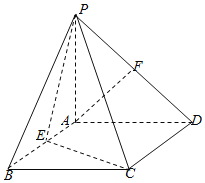
(Ⅰ)求证:AF∥平面PEC;
(Ⅱ)求证:平面PEC⊥平面PCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com