Question

【题目】已知椭圆右焦点，离心率为，过作两条互相垂直的弦，设中点分别为.

（1）求椭圆的方程；

(2) 证明：直线必过定点，并求出此定点坐标；

(3) 若弦的斜率均存在，求面积的最大值．

Answer 1

【答案】（1）；（2）直线MN过定点；（3）S△FMN的最大值为.

【解析】分析：（1）根据题意确定出c与e的值，利用离心率公式求出a的值，进而求出b的值，确定出椭圆方程即可；

（2）由直线AB与CD斜率均存在，设为k，表示出AB方程，设出A与B坐标，联立直线AB与椭圆方程，消去y得到关于x的一元二次方程，利用根与系数的关系表示出M，同理表示出N，根据M与N横坐标相同求出k的值，得到此时MN斜率不存在，直线MN恒过定点；若直线MN斜率存在，表示出直线MN斜率，进而表示出直线MN，令y=0，求出x的值，得到直线MN恒过定点，综上，得到直线MN恒过定点，求出定点坐标即可；

（3）根据P坐标，得到OP的长，由OF﹣OP表示出PF长，S△FMN＝S△FPM＋S△FPN，利用基本不等式求出面积的最大值即可．

详解：(1) （1）由题意：c=1， =，

∴a=，b=c=1，

则椭圆的方程为+y2=1；

(2) ∵AB，CD斜率均存在，

∴设直线AB方程为：y=k（x﹣1），

再设A（x1，y1），B（x2，y2），则有M（，k（﹣1）），

联立得： ，

消去y得：（1+2k2）x2﹣4k2x+2k2﹣2=0，

∴，即M（， ），

将上式中的k换成﹣，同理可得：N（， ），

若=，解得：k=±1，直线MN斜率不存在，

此时直线MN过点（，0）；

下证动直线MN过定点P（，0），

若直线MN斜率存在，则kMN===×，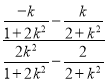

直线MN为y﹣=×（x﹣），

令y=0，得x=+×=×=，

综上，直线MN过定点（，0）；

(3) 由第（2）问可知直线MN过定点P（，0），

故S△FMN=S△FPM+S△FPN=×||+×|=×，

令t=|k|+∈[2，+∞），S△FMN=f（t）=×=×，

∴f（t）在t∈[2，+∞）单调递减，

当t=2时，f（t）取得最大值，即S△FMN最大值，此时k=±1．