
【题目】如图,在四棱柱![]() 中,侧面
中,侧面![]() ⊥底面
⊥底面![]() ,
,![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]()
![]() ,O为
,O为![]() 中点.
中点.
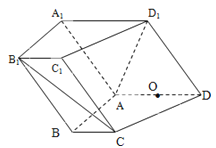
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求锐二面角A—C1D1—C的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]()
【解析】
(I)证明![]() ,即证:四边形AB1CO为平行四边形.
,即证:四边形AB1CO为平行四边形.
(II)![]() 为
为![]() 的中点,
的中点,![]() ,又侧面
,又侧面![]() ⊥底面
⊥底面![]() ,故
,故![]() ⊥底面
⊥底面![]() ,然后建立直角坐标系,利用向量法求二面角,先求二面角两个面的法向量,然后再求法向量的夹角,根据法向量的夹角与二面角相等或互补来解.
,然后建立直角坐标系,利用向量法求二面角,先求二面角两个面的法向量,然后再求法向量的夹角,根据法向量的夹角与二面角相等或互补来解.
(Ⅰ)证明:如图,连接![]() ,
,
则四边形![]() 为正方形,
为正方形,
![]() ,且
,且![]()
故四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
(Ⅱ)![]() 为
为![]() 的中点,
的中点,![]() ,又侧面
,又侧面![]() ⊥底面
⊥底面![]() ,故
,故![]() ⊥底面
⊥底面![]() ,
,

以![]() 为原点,所
为原点,所![]() 在直线分别为
在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的坐标系,则
轴建立如图所示的坐标系,则![]()
![]() ,
,
![]()
![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,由
的一个法向量,由![]() ,得
,得![]() ,
,
令![]() ,则
,则![]()
又设![]() 为平面
为平面![]() 的一个法向量,由
的一个法向量,由![]() ,得
,得![]() ,令
,令
![]() ,则
,则![]() ,
,
则![]() ,故所求锐二面角A—C1D1—C的余弦值为
,故所求锐二面角A—C1D1—C的余弦值为![]()
注:第2问用几何法做的酌情给分.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() :
:![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的任意一点,射线
上的任意一点,射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,直线
有且只有一个公共点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两个相异点,证明:
两个相异点,证明:![]() 面积为定值.
面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.抛掷一枚硬币,正面朝上的概率是![]() ,所以抛掷两次一定会出现一次正面朝上的情况
,所以抛掷两次一定会出现一次正面朝上的情况
B.某地气象局预报说,明天本地降水概率为![]() ,这说明明天本地有
,这说明明天本地有![]() 的区域下雨
的区域下雨
C.概率是客观存在的,与试验次数无关
D.若买彩票中奖的概率是万分之一,则买彩票一万次就有一次中奖
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,右焦点为
,右焦点为![]() ,且
,且![]() 上的动点
上的动点![]() 到
到![]() 的距离的最大值为4,最小值为2.
的距离的最大值为4,最小值为2.
(1)证明:![]() .
.
(2)若直线![]() :
:![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 均不与
均不与![]() ,
,![]() 重合),且
重合),且![]() ,试问
,试问![]() 是否经过定点?若经过,求出此定点坐标;若不经过,请说明理由.
是否经过定点?若经过,求出此定点坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是国家统计局今年4月11日发布的2018年3月到2019年3月全国居民消费价格的涨跌幅情况折线图.(注:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比),根据该折线图,下列结论错误的是
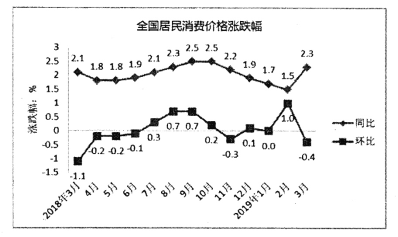
A. 2018年3月至2019年3月全国居民消费价格同比均上涨
B. 2018年3月至2019年3月全国居民消费价格环比有涨有跌
C. 2019年3月全国居民消费价格同比涨幅最大
D. 2019年3月全国居民消费价格环比变化最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知z,y之间的一组数据如下表:
x | 1 | 3 | 6 | 7 | 8 |
y | 1 | 2 | 3 | 4 | 5 |
(1)从x ,y中各取一个数,求x+y≥10的概率;
(2)对于表中数据,甲、乙两同学给出的拟合直线分别为![]() 与
与![]() ,试利用“最小平方法(也称最小二乘法)”判断哪条直线拟合程度更好.
,试利用“最小平方法(也称最小二乘法)”判断哪条直线拟合程度更好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分
沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时。如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的![]() (细管长度忽略不计).
(细管长度忽略不计).

(1)如果该沙漏每秒钟漏下0.02cm3的沙,则该沙漏的一个沙时为多少秒(精确到1秒)?
(2)细沙全部漏入下部后,恰好堆成个一盖住沙漏底部的圆锥形沙堆,求此锥形沙堆的高度(精确到0.1cm).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com