练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某企业想通过做广告来提高销售额，经预测可知本企业产品的广告费x（单位：百万元）与销售额y（单位：百万元）之间有如下对应数据：

    x

    2

    4

    5

    6

    8

    y

    30

    40

    60

    50

    70

    由表中的数据得线性回归方程为 = x+ ，其中 =6.5，由此预测当广告费为7百万元时，销售额为万元．

    【答案】6300
    【解析】解：样本平均数 = =5， = =50．

    ∴ （xi﹣ ）（yi﹣ ）=﹣3×（﹣20）+（﹣1）×（﹣10）+0+0+3×20=130，

    （xi﹣ ）2=9+1+0+1+9=20，

    ∴ = ，

    ∴ =50﹣6.5×5=7.5．

    线性回归方程为：y=6.5x+17.5，

    预测当广告费为7百万元时，即x=7时，y=63百万元．

    所以答案是：6300．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动，其路程关于时间的函数关系式分别为，，，，有以下结论：

    ①当时，甲走在最前面；

    ②当时，乙走在最前面；

    ③当时，丁走在最前面，当时，丁走在最后面；

    ④丙不可能走在最前面，也不可能走在最后面；

    ⑤如果它们一直运动下去，最终走在最前面的是甲．

    其中，正确结论的序号为 （把正确结论的序号都填上，多填或少填均不得分）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在上的函数满足：对任意、恒成立，当时，.

    （1）求证在上是单调递增函数；

    （2）已知，解关于的不等式；

    （3）若，且不等式对任意恒成立.求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场出售两款型号不同的手机，由于市场需求发生变化，第一款手机连续两次提价10%，第二款手机连续两次降价10%，结果都以1210元出售．

    (1)求第一款手机的原价；

    (2)若该商场同时出售两款手机各一部，求总售价与总原价之间的差额．(结果精确到整数)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了考察某种中成药预防流感的效果，抽样调查40人，得到如下数据

    患流感

    未患流感

    服用药

    2

    18

    未服用药

    8

    12

    根据表中数据，通过计算统计量K2= ，并参考以下临界数据：

    P（K2＞k0）

    0.50

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k0

    0.455

    0.708

    1.323

    2.072

    2.706

    3.84

    5.024

    6.635

    7.879

    10.828

    若由此认为“该药物有效”，则该结论出错的概率不超过（ ）
    A.0.05
    B.0.025
    C.0.01
    D.0.005

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，直线C1的参数方程为 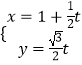（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ2（1+2sin2θ）=3．
    （Ⅰ）写出C1的普通方程和C2的直角坐标方程；
    （Ⅱ）直线C1与曲线C2相交于A，B两点，点M（1，0），求||MA|﹣|MB||．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C的方程为 + =1（a＞b＞0），双曲线 ﹣ =1的一条渐近线与x轴所成的夹角为30°，且双曲线的焦距为4 ．

    （1）求椭圆C的方程；
    （2）过右焦点F的直线l，交椭圆于A、B两点，记△AOF的面积为S1 ， △BOF的面积为S2 ， 当S1=2S2时，求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】第35届牡丹花会期间，我班有5名学生参加志愿者服务，服务场所是王城公园和牡丹公园．
    （1）若学生甲和乙必须在同一个公园，且甲和丙不能在同一个公园，则共有多少种不同的分配方案？
    （2）每名学生都被随机分配到其中的一个公园，设X，Y分别表示5名学生分配到王城公园和牡丹公园的人数，记ξ=|X﹣Y|，求随机变量ξ的分布列和数学期望E（ξ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，O为坐标原点，A，B，C三点满足。

    （1）求证：A，B，C三点共线；

    （2）若A（1，cosx），B（1+sinx，cosx），且x∈[0， ]，函数f（x）=（2m+）||+m2的最小值为5，求实数m的值。

    查看答案和解析>>

    同步练习册答案