
【题目】已知平面上两定点M(0,﹣2)、N(0,2),P为一动点,满足![]()
![]() |
|![]() ||
||![]() |
|
(I)求动点P的轨迹C的方程;
(II)若A、B是轨迹C上的两不同动点,且![]() λ
λ![]() .分别以A、B为切点作轨迹C的切线,设其交点Q,证明
.分别以A、B为切点作轨迹C的切线,设其交点Q,证明![]() 为定值.
为定值.
【答案】(I)x2=8y
(II)见解析
【解析】
(I)先设P(x,y),求动点P的轨迹C的方程,即寻找x,y之间的关系,结合向量的坐标运算即可得到.
(II)先设出A,B两点的坐标,利用向量关系及向量运算法则,用A,B的坐标表示出![]() ,最后看其是不是定值即可.
,最后看其是不是定值即可.
(I)设P(x,y).
由已知 ![]() (x,y+2),
(x,y+2),![]() (0,4),
(0,4),![]() (﹣x,2﹣y),
(﹣x,2﹣y),
![]()
![]() 4y+8.
4y+8.
|![]() ||
||![]() |=4
|=4![]()
∵![]()
![]() |
|![]() ||
||![]() |
|
∴4y+8=4![]() 整理,得x2=8y
整理,得x2=8y
即动点P的轨迹C为抛物线,其方程为x2=8y.
(II)由已知N(0,2).
即得(﹣x1,2﹣y1)=λ(x2,y2﹣2)
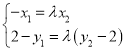
设A(x1,y1),B(x2,y2).由![]() λ
λ![]()
即得(﹣x1,2﹣y1)=λ(x2,y2﹣2),
∴﹣x1=λx2…(1),
2﹣y1=λ(y2﹣2)…(2)
将(1)式两边平方并把x12=8y1,x2/span>2=8y2代入得y1=![]() y2
y2
解得 y1=2λ,y2![]() ,
,
且有x1x2=﹣λx22=﹣8λy2=﹣16.
抛物线方程为 y=![]() ,求导得y′
,求导得y′![]() x.
x.
所以过抛物线上A、B两点的切线方程分别是 y![]() x1(x﹣x1)+y1,y
x1(x﹣x1)+y1,y![]() x2(x﹣x2)+y2,
x2(x﹣x2)+y2,
即y![]() x1x
x1x![]() x12,y
x12,y![]() x2x
x2x![]() x22
x22
解出两条切线的交点Q的坐标为 (![]() ,
,![]() )=(
)=(![]() ,﹣2)
,﹣2)
所以 ![]()
![]() (
(![]() ,﹣4)(x2﹣x1,y1﹣y2)
,﹣4)(x2﹣x1,y1﹣y2)
![]() (x22﹣x12)﹣4(
(x22﹣x12)﹣4(![]() x22
x22![]() x12)=0
x12)=0
所以 ![]() 为定值,其值为0.
为定值,其值为0.


科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在![]() 上的单调函数,且对任意的x∈
上的单调函数,且对任意的x∈![]() 都有
都有![]() ,则方程
,则方程![]() 的一个根所在的区间是( )
的一个根所在的区间是( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下列四个结论:
有下列四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 的最小正周期为
的最小正周期为![]() ;③
;③![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的值域为
的值域为![]() .
.
上述结论中,正确的为( )
A.③④B.②④C.①③D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花.若BC=a,∠ABC=![]() ,设△ABC的面积为S1,正方形的面积为S2.
,设△ABC的面积为S1,正方形的面积为S2.
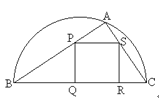
(1)用a,![]() 表示S1和S2;
表示S1和S2;
(2)当a固定,![]() 变化时,求
变化时,求![]() 取最小值时的角
取最小值时的角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,过点
的焦点,过点![]() 任作两条互相垂直的直线
任作两条互相垂直的直线![]() ,
,![]() ,分别交抛物线
,分别交抛物线![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四点,
四点,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
(1)求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(2)设直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,试求
两点,试求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com