
【题目】设函数f(x)=4sinx(cosx﹣sinx)+3 (Ⅰ)当x∈(0,π)时,求f(x)的单调递减区间;
(Ⅱ)若f(x)在[0,θ]上的值域为[0,2 ![]() +1],求cos2θ的值.
+1],求cos2θ的值.
【答案】解:(Ⅰ)函数f(x)=4sinx(cosx﹣sinx)+3
=4sinxcosx﹣4sin2x+3
=2sin2x﹣4× ![]() +3
+3
=2sin2x+2cos2x+1
=2 ![]() sin(2x+
sin(2x+ ![]() )+1,
)+1,
令2kπ+ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
解得kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
又x∈(0,π),
所以f(x)的单调递减区间是[ ![]() ,
, ![]() ];
];
(Ⅱ)由f(x)=2 ![]() sin(2x+
sin(2x+ ![]() )+1在[0,θ]上的值域为[0,2
)+1在[0,θ]上的值域为[0,2 ![]() +1],
+1],
令x=0,得f(0)=2 ![]() sin
sin ![]() +1=3;
+1=3;
令f(x)=2 ![]() +1,得sin(2x+
+1,得sin(2x+ ![]() )=1,
)=1,
解得x= ![]() ,∴θ>
,∴θ> ![]() ;
;
令f(x)=0,得sin(2x+ ![]() )=﹣
)=﹣ ![]() ,
,
∴2x+ ![]() <
< ![]() ,
,
解得x< ![]() ,即θ<
,即θ< ![]() ;
;
∴θ∈( ![]() ,
, ![]() ),
),
∴2θ+ ![]() ∈(
∈( ![]() ,
, ![]() );
);
由2 ![]() sin(2θ+
sin(2θ+ ![]() )+1=0,
)+1=0,
得sin(2θ+ ![]() )=﹣
)=﹣ ![]() ,
,
所以cos(2θ+ ![]() )=﹣
)=﹣ 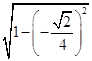 =﹣
=﹣ ![]() ,
,
所以cos2θ=cos[(2θ+ ![]() )﹣
)﹣ ![]() ]
]
=cos(2θ+ ![]() )cos
)cos ![]() +sin(2θ+
+sin(2θ+ ![]() )sin
)sin ![]()
=﹣ ![]() ×
× ![]() +(﹣
+(﹣ ![]() )×
)× ![]()
=﹣ ![]() .
.
【解析】(Ⅰ)化简函数f(x)为正弦型函数,根据正弦函数的图象与性质即可求出f(x)的单调减区间;(Ⅱ)根据题意,求出sin(2θ+ ![]() )的值,再根据同角的三角函数关系和三角恒等变换求出cos2θ的值.
)的值,再根据同角的三角函数关系和三角恒等变换求出cos2θ的值.
【考点精析】根据题目的已知条件,利用正弦函数的单调性的相关知识可以得到问题的答案,需要掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数.
上是减函数.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为 ![]() . (Ⅰ)求椭圆C的方程;
. (Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为 ![]() ,求△AOB面积的最大值.
,求△AOB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数集R,集合A={x|1<x<3},集合B={x|y= ![]() },则A∩(RB)=( )
},则A∩(RB)=( )
A.{x|1<x≤2}
B.{x|1<x<3}
C.{x|2≤x<3}
D.{x|1<x<2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(﹣ ![]() ,
, ![]() ),∠AOB=α.
),∠AOB=α. 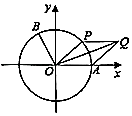
(1)求 ![]() 的值;
的值;
(2)设∠AOP=θ( ![]() ≤θ≤
≤θ≤ ![]() ),
), ![]() =
= ![]() +
+ ![]() ,四边形OAQP的面积为S,f(θ)=(
,四边形OAQP的面积为S,f(θ)=( ![]()
![]() ﹣
﹣ ![]() )2+2S2﹣
)2+2S2﹣ ![]() ,求f(θ)的最值及此时θ的值.
,求f(θ)的最值及此时θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣x2 , 若存在实数a,b,使f(x)在[a,b]上的值域为[ ![]() ,
, ![]() ],则ab= .
],则ab= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义min{a,b}= ![]() ,若函数f(x)=min{x2﹣3x+3,﹣|x﹣3|+3},且f(x)在区间[m,n]上的值域为[
,若函数f(x)=min{x2﹣3x+3,﹣|x﹣3|+3},且f(x)在区间[m,n]上的值域为[ ![]() ,
, ![]() ],则区间[m,n]长度的最大值为( )
],则区间[m,n]长度的最大值为( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组中的函数f(x),g(x)表示同一函数的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)=x+1,g(x)= ![]()
C.f(x)=|x|,g(x)= ![]()
D.f(x)=log22x , g(x)=2log2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x的图象与函数y=g(x)的图象关于直线y=x对称.
)x的图象与函数y=g(x)的图象关于直线y=x对称.
(1)若f(g(x))=6﹣x2 , 求实数x的值;
(2)若函数y=g(f(x2))的定义域为[m,n](m≥0),值域为[2m,2n],求实数m,n的值;
(3)当x∈[﹣1,1]时,求函数y=[f(x)]2﹣2af(x)+3的最小值h(a).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com