练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】把函数的图象向右平移个单位长度，再把所得的函数图象上所有点的横坐标缩短到原来的（纵坐标不变）得到函数的图象，关于的说法有：①函数的图象关于点对称；②函数的图象的一条对称轴是；③函数在上的最上的最小值为；④函数上单调递增，则以上说法正确的个数是（ ）

    A.4个B.3个C.2个D.1个

    【答案】C

    【解析】

    通过平移变换与伸缩变换求得函数的解析式.由判断①错误；由求得最小值判断②正确；由x的范围求得函数值域判断③正确；由x的范围可知函数在上不单调判断④错误.

    把函数的图象向右平移个单位长度，得，

    再把所得的函数图象上所有点的横坐标缩短到原来的（纵坐标不变）得到函数的图象，

    则.

    ①∵，∴函数的图象不关于点对称，故①错误；

    ②∵，∴函数的图象的一条对称轴是，故②正确；

    ③当时，，则，即函数在上的最上的最小值为，故③正确；

    ④当时，，可知函数在上不单调，故④错误.

    ∴正确命题的个数为2.

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】中国是茶的故乡，也是茶文化的发源地.中国茶的发现和利用已有四千七百多年的历史，且长盛不衰，传遍全球.为了弘扬中国茶文化，某酒店推出特色茶食品“金萱排骨茶”，为了解每壶“金萱排骨茶”中所放茶叶量克与食客的满意率的关系，通过试验调查研究，发现可选择函数模型来拟合与的关系，根据以下数据：

    茶叶量克

    1

    2

    3

    4

    5

    4.34

    4.36

    4.44

    4.45

    4.51

    可求得y关于x的回归方程为（ ）

    A.B.

    C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，由经过伸缩变换得到曲线，以原点为极点，轴非负半轴为极轴，建立极坐标系，曲线的极坐标方程为．

    （1）求曲线的极坐标方程以及曲线的直角坐标方程；

    （2）若直线的极坐标方程为，与曲线、曲线在第一象限交于、，且，点的极坐标为，求的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，某街道居委会拟在地段的居民楼正南方向的空白地段上建一个活动中心，其中米．活动中心东西走向，与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形，上部分是以为直径的半圆. 为了保证居民楼住户的采光要求，活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长不超过米，其中该太阳光线与水平线的夹角满足.

    （1）若设计米，米，问能否保证上述采光要求？

    （2）在保证上述采光要求的前提下，如何设计与的长度，可使得活动中心的截面面积最大？（注：计算中取3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线 和点D(2,0)，直线 与抛物线C交于不同两点A、B，直线BD与抛物线C交于另一点E.给出以下判断：

    ①直线OB与直线OE的斜率乘积为-2； ②轴； ③以BE为直径的圆与抛物线准线相切；

    其中，所有正确判断的序号是（ ）

    A.①②③B.①②C.①③D.②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】张师傅欲将一球形的石材工件削砍加工成一圆柱形的新工件，已知原球形工件的半径为，则张师傅的材料利用率的最大值等于（注：材料利用率=）（ ）

    A. B. C. D.

    【答案】C

    【解析】设球半径为R，圆柱的体积为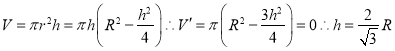时圆柱的体积最大为 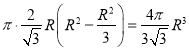,因此材料利用率= 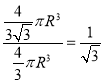,选C.

    点睛:空间几何体与球接、切问题的求解方法

    求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．

    【题型】单选题
    【结束】
    12

    【题目】已知抛物线： 在点处的切线与曲线： 相切，若动直线分别与曲线、相交于、两点，则的最小值为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的离心率，且圆过椭圆的上，下顶点.

    （1）求椭圆的方程.

    （2）若直线的斜率为，且直线交椭圆于、两点，点关于点的对称点为，点是椭圆上一点，判断直线与的斜率之和是否为定值，如果是，请求出此定值：如果不是，请说明理.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆过点，且其离心率为，过坐标原点作两条互相垂直的射线与椭圆分别相交于，两点.

    （1）求椭圆的方程；

    （2）是否存在圆心在原点的定圆与直线总相切？若存在，求定圆的方程；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（理）某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在内，发布成绩使用等级制各等级划分标准见下表，规定：三级为合格等级，为不合格等级.

    百分制

    85分及以上

    70分到84分

    60分到69分

    60分以下

    等级

    为了解该校高一年级学生身体素质情况，从中抽取了名学生的原始成绩作为样本进行统计，按照的分组作出频率分布直方图如图所示，样本中分数在80分及以上的所有数据的茎叶图如图所示.，

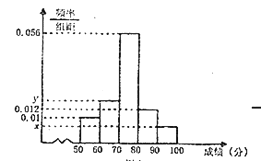
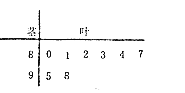
    （1）求和频率分布直方图中的的值；

    （2）根据样本估计总体的思想，以事件发生的频率作为相应事件发生的概率，若在该校高一学生任选3人，求至少有1人成绩是合格等级的概率；

    （3）在选取的样本中，从两个等级的学生中随机抽取了3名学生进行调研，记表示所抽取的名学生中为等级的学生人数，求随机变量的分布列及数学期望.

    查看答案和解析>>

    同步练习册答案