
若满足条件C=60°,AB=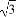 ,BC=a的△ABC有两个,那么a的取值范围是( )
,BC=a的△ABC有两个,那么a的取值范围是( )
(A)(1,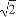 ) (B)(
) (B)(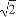 ,
,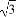 )
)
(C)(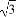 ,2) (D)(1,2)
,2) (D)(1,2)
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十八第四章第四节练习卷(解析版) 题型:解答题
已知A,B,C三点的坐标分别为A(3,0),B(0,3),C(cosα,sinα),其中α∈(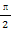 ,
,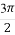 ).
).
(1)若|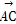 |=|
|=|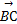 |,求角α的值.
|,求角α的值.
(2)若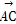 ·
·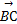 =-1,求tan(α+
=-1,求tan(α+ )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十二第三章第六节练习卷(解析版) 题型:选择题
已知函数f(x)=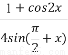 -asin
-asin cos(π-
cos(π- )的最大值为2,则常数a的值为( )
)的最大值为2,则常数a的值为( )
(A)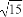 (B)-
(B)-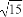
(C)±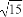 (D)±
(D)±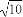
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十九第四章第五节练习卷(解析版) 题型:选择题
已知复数z=1+i,则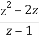 等于( )
等于( )
(A)2i(B)-2i(C)2(D)-2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十三第三章第七节练习卷(解析版) 题型:解答题
在△ABC中,a,b,c分别为角A,B,C的对边.已知a=1,b=2,sinC=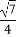 (其中C为锐角).
(其中C为锐角).
(1)求边c的值.
(2)求sin(C-A)的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十七第四章第三节练习卷(解析版) 题型:解答题
在平面直角坐标系中,已知向量a=(-1,2),又点A(8,0),B(n,t),C(ksinθ,t)(0≤θ≤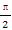 ).
).
(1)若 ⊥a,且|
⊥a,且| |=
|=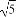 |
|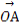 |(O为坐标原点),求向量
|(O为坐标原点),求向量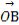 .
.
(2)若向量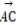 与向量a共线,当k>4,且tsinθ取最大值4时,求
与向量a共线,当k>4,且tsinθ取最大值4时,求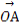 ·
·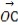 .
.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十七第四章第三节练习卷(解析版) 题型:选择题
已知a,b,c为△ABC的三个内角A,B,C的对边,向量m=(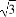 ,-1),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角A,B的大小分别为( )
,-1),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角A,B的大小分别为( )
(A)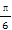 ,
,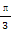 (B)
(B)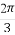 ,
,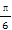
(C)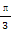 ,
,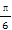 (D)
(D)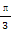 ,
,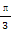
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十一第三章第五节练习卷(解析版) 题型:选择题
设sin( +θ)=
+θ)= ,则sin2θ等于( )
,则sin2θ等于( )
(A)- (B)
(B)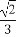 (C)
(C) (D)
(D)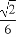
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com