分析:(I)根据函数
y=Asin(ωx+φ),(A>0,ω>0,|φ|<)相邻的两个最高点和最低点分别为,可分析出函数的最值,确定A的值,分析出函数的周期,确定ω的值,将
(,2)代入解析式,结合
|φ|<,可求出φ值,进而求出函数的解析式.
(II)由2x+
∈[
+2kπ,
+2kπ],k∈Z,求出自变量的取值范围,可得函数的单调递减区间;
(Ⅲ)由
x∈[0,],求出相位角2x+
的取值范围,进而根据正弦函数的图象求出最值,可得函数的值域.
解答:解:(I)由函数图象相邻的两个最高点和最低点分别为
(,2),(,-2)∵A>0
∴A=2
∵
=
-=
,ω>0
∴ω=2
∴y=2sin(2x+φ)
将
(,2)代入y=2sin(2x+φ)得sin(
+φ)=1
即
+φ=
+2kπ,k∈Z
即φ=
+2kπ,k∈Z
∵
|φ|<∴
φ=∴函数表达式为2sin(2x+
)
(II)由2x+
∈[
+2kπ,
+2kπ],k∈Z,得
x∈[
+2kπ,
+2kπ],k∈Z,
∴函数的单调递减区间为[
+2kπ,
+2kπ],k∈Z,
(III)当
x∈[0,]时,
2x+
∈[
,
]
当2x+
=
,即x=
时,函数取最大值2
当2x+
=
时,即x=
时,函数取最小值-1
∴函数的值域为[-1,2]
点评:本题考查的知识点是正弦型函数的解析式求法,正弦型函数的单调区间,正弦型函数在定区间上的值域,熟练掌握正弦型函数的图象和性质是解答本题的关键.



 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案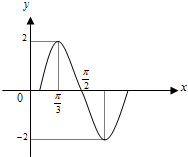 已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )
已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )