
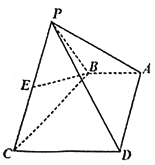
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,
,![]() 是边长为2的正三角形,求点
是边长为2的正三角形,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析.(2)![]() .
.
【解析】分析:第一问首先在平面![]() 内寻找
内寻找![]() 的平行线,这个任务借助中位线,从而取
的平行线,这个任务借助中位线,从而取![]() 中点
中点![]() ,
,![]() 即为所求,之后应用线面平行的判定定理证得结果;第二问利用线面平行将点
即为所求,之后应用线面平行的判定定理证得结果;第二问利用线面平行将点![]() 到平面
到平面![]() 的距离转化为求点
的距离转化为求点![]() 到平面
到平面![]() 的距离,之后用等级法,借助于三棱锥
的距离,之后用等级法,借助于三棱锥![]() 的体积和三棱锥
的体积和三棱锥![]() 的体积相等求得对应的高,即点到面的距离.
的体积相等求得对应的高,即点到面的距离.
详解:(1)证明:取![]() 的中点
的中点![]() ,连结
,连结![]()
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,且
,且![]()
又∵![]() ,且
,且![]()
∴![]() ,且
,且![]() ,故四边形
,故四边形![]() 为平行四边形
为平行四边形
∴![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)由(1)得![]() 平面
平面![]()
故点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离
的距离
取![]() 的中点
的中点![]() ,连结
,连结![]()
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]()
又![]() 是边长为2的正三角形
是边长为2的正三角形
∴![]() ,
,![]() ,且
,且![]()
∵平面![]() 平面
平面![]()
∴![]() 平面
平面![]() ,
,
∵四边形是直角梯形,![]()
∴![]()
∵![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
记点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
∵三棱锥![]() 的体积
的体积![]()
∴![]() .
.
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,如图1.以
,如图1.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
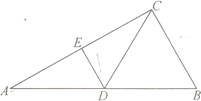

如图1 如图2
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,当
,当![]() 时,
时,![]() .
.
(Ⅰ)若函数![]() 过点
过点![]() ,求此时函数
,求此时函数![]() 的解析式;
的解析式;
(Ⅱ)若函数![]() 只有一个零点,求实数
只有一个零点,求实数![]() 的值;
的值;
(Ⅲ)设![]() ,若对任意实数
,若对任意实数![]() ,函数
,函数![]() 在
在![]() 上的最大值与最小值的差不大于1,求实数
上的最大值与最小值的差不大于1,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为原点,其焦点
的顶点为原点,其焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() .设
.设![]() 为直线
为直线![]() 上的点,过点
上的点,过点![]() 作抛物线
作抛物线![]() 的两条切线
的两条切线![]() ,其中
,其中![]() 为切点.
为切点.
(1) 求抛物线![]() 的方程;
的方程;
(2) 当点![]() 为直线
为直线![]() 上的定点时,求直线
上的定点时,求直线![]() 的方程;
的方程;
(3) 当点![]() 在直线
在直线![]() 上移动时,求
上移动时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的班车在8:00准时发车,小田与小方均在7:40至8:00之间到达发车点乘坐班车,且到达发车点的时刻是随机的,则小田比小方至少早5分钟到达发车点的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 的方程为
的方程为![]() .
.
(1)若![]() 在两坐标轴上的截距相等,求
在两坐标轴上的截距相等,求![]() 的方程;
的方程;
(2)若![]() 不经过第二象限,求实数
不经过第二象限,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,与
,与![]() 轴负半轴的交点为
轴负半轴的交点为![]() ,求
,求![]() (
(![]() 为坐标原点)面积的最小值.
为坐标原点)面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com