解:(1)求导函数可得f'(x)=
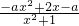
①当a=0时,f'(x)>0时x>0,即函数f(x)在(0,+∞)上单调递增,f'(x)<0时x<0,即函数f(x)在(-∞,0)上单调递减;
②当a≠0且|a|≤1时,由f'(x)=0,得ax
2-2x+a=0,∴
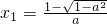
,
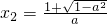
1°a=1时,f'(x)≤0,∴函数f(x)在R上单调递减;
2°a=-1时,f'(x)≥0,∴函数f(x)在R上单调递增;
3°当-1<a<0时,由f'(x)>0可得x<x
1或x>x
2,即函数f(x)在(-∞,
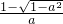
)、(
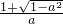
,+∞)上单调递增,在(
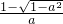
,
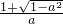
)上单调递减;
4°当0<a<1时,由f'(x)>0可得x
1<x<x
2,即函数f(x)在(
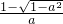
,
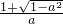
)上单调递增,在(-∞,
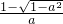
)、(
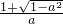
,+∞)上单调递减;
(2)f(x)的图象与g(x)的图象恰有四个不同的交点,则f(x)=g(x)有四个根,即a=ln(x
2+1)-
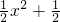
令G(x)=ln(x
2+1)-
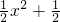
,则 G′(x)=

| x | (-∞,-1) | -1 | (-1,0) | 0 | (0,1) | 1 | (1,+∞) |
| G′(x) | + | 0 | - | 0 | + | | |
| G(x) | | ln2 | |  | | ln2 | |
∴x=0时,函数取得极小值

,x=±1时,函数确定极大值 ln2
∴a∈(

,ln2).
分析:(1)求导函数,对a进行分类讨论:①当a=0时,f'(x)>0时x>0,f'(x)<0时x<0;②当a≠0且|a|≤1时,考虑a=1,a=-1,-1<a<0,0<a<1利用导数的正负,可得函数的单调区间;
(2)f(x)的图象与g(x)的图象恰有四个不同的交点,则f(x)=g(x)有四个根,即a=ln(x
2+1)-
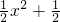
,构造新函数,确定函数的极值,即可求得a的取值范围.
点评:本题考查导数知识的运用,考查函数的单调性,考查分类讨论的数学思想,考查函数图象的交点,考查函数的极值,综合性强.

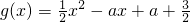 ,是否存在实数a使得f(x)的图象与g(x)的图象恰有四个不同的交点,若存在,求a的取值范围;否则,说明理由.
,是否存在实数a使得f(x)的图象与g(x)的图象恰有四个不同的交点,若存在,求a的取值范围;否则,说明理由.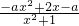
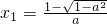 ,
,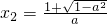
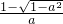 )、(
)、(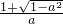 ,+∞)上单调递增,在(
,+∞)上单调递增,在(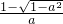 ,
,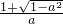 )上单调递减;
)上单调递减;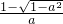 ,
,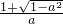 )上单调递增,在(-∞,
)上单调递增,在(-∞,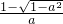 )、(
)、(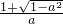 ,+∞)上单调递减;
,+∞)上单调递减; 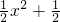
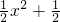 ,则 G′(x)=
,则 G′(x)=

 ,x=±1时,函数确定极大值 ln2
,x=±1时,函数确定极大值 ln2 ,ln2).
,ln2).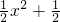 ,构造新函数,确定函数的极值,即可求得a的取值范围.
,构造新函数,确定函数的极值,即可求得a的取值范围.
