
【题目】为了美化校园,要对校园内某一区域作如下设计,如图,已知![]() ,
,![]() ,
,![]() ,在边BC上选一点P. 沿着AP和CP重新栽种花木,图中阴影部分铺上草坪. AP段栽种花木费用是每米3a元,CP段栽种花木费用是每米2a元,其中a是正常数.设
,在边BC上选一点P. 沿着AP和CP重新栽种花木,图中阴影部分铺上草坪. AP段栽种花木费用是每米3a元,CP段栽种花木费用是每米2a元,其中a是正常数.设![]() .
.
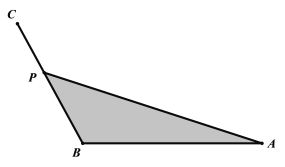
(1)求栽种花木费用y关于θ的函数表达式;
(2)求![]() 的值,使得栽种花木费用y最小.
的值,使得栽种花木费用y最小.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
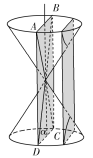
【题目】古希腊数学家阿波罗尼斯在他的著作《圆锥曲线论》中记载了用平面切割圆锥得到圆锥曲线的方法.如图,将两个完全相同的圆锥对顶放置(两圆锥的轴重合),已知两个圆锥的底面半径均为1,母线长均为3,记过圆锥轴的平面![]() 为平面
为平面![]() (
(![]() 与两个圆锥侧面的交线为
与两个圆锥侧面的交线为![]() ),用平行于
),用平行于![]() 的平面截圆锥,该平面与两个圆锥侧面的交线即双曲线
的平面截圆锥,该平面与两个圆锥侧面的交线即双曲线![]() 的一部分,且双曲线
的一部分,且双曲线![]() 的两条渐近线分别平行于
的两条渐近线分别平行于![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 点
点![]() 是椭圆上任意一点,且
是椭圆上任意一点,且![]() 的最大值为4,椭圆
的最大值为4,椭圆![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数.
的离心率互为倒数.
(1)求椭圆方程;
(2)设点![]() ,过点
,过点![]() 作直线
作直线![]() 与圆
与圆![]() 相切且分别交椭圆于
相切且分别交椭圆于![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到![]() 的图象
的图象![]() ,只要将
,只要将![]() 图象
图象![]() 怎样变化得到( )
怎样变化得到( )
A.将![]() 的图象
的图象![]() 沿x轴方向向左平移
沿x轴方向向左平移![]() 个单位
个单位
B.将![]() 的图象
的图象![]() 沿x轴方向向右平移
沿x轴方向向右平移![]() 个单位
个单位
C.先作![]() 关于x轴对称图象
关于x轴对称图象![]() ,再将图象
,再将图象![]() 沿x轴方向向右平移
沿x轴方向向右平移![]() 个单位
个单位
D.先作![]() 关于x轴对称图象
关于x轴对称图象![]() ,再将图象
,再将图象![]() 沿x轴方向向左平移
沿x轴方向向左平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】拉丁舞,又称拉丁风情舞或自由社交舞,它是拉丁人民在漫长的历史长河中形成的,包含伦巴、恰恰、牛仔舞、桑巴、斗牛舞、深受人民的喜爱.某艺术培训机构为了调查本校学院对拉丁舞的学习情况,分别在刚学习了一个季度的本校大班(8岁以下)及种子班(8岁以上)的学员中各随机抽取了15名学员进行摸底考试,这30名学员考试成绩的茎叶图如图所示.

规定:成绩不低于85分,则认为成绩优秀;成绩低于85分,则认为成绩一般.
(1)根据上述数据填写下列2×2联表:
成绩优秀 | 成绩一般 | 总计 | |
大班 | |||
种子班 | |||
总计 |
判断是否有95%的把握认为成绩优秀或成绩一般与学员的年龄有关;
(2)在大班及种子班的参加摸底考试且成绩优秀的学员中以分层抽样的方式抽取6名学员进行特别集训,集训后,再对这6名学员进行测试,按测试成绩,取前3名授予“舞蹈小精灵”称号,在被授予“舞蹈小精灵”称号的学员中,求种子班的学员恰好有2人的概率.
参考公式及数据: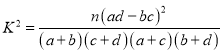 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com