
【题目】已知函数![]() (
(![]() 为自然对数的底数)
为自然对数的底数)
(1)若曲线![]() 在点
在点![]() 处的切线平行于
处的切线平行于![]() 轴,求
轴,求![]() 的值;
的值;
(2)求函数![]() 的极值;
的极值;
(3)当![]() 时,若直线
时,若直线![]() 与曲线
与曲线![]() 没有公共点,求
没有公共点,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)当
(2)当![]() 时,函数
时,函数![]() 无极小值;当
无极小值;当![]() ,
,![]() 在
在![]() 处取得极小值
处取得极小值![]() ,无极大值(3)
,无极大值(3)![]() 的最大值为
的最大值为![]()
【解析】
(1)求出![]() ,由导数的几何意义,解方程
,由导数的几何意义,解方程![]() 即可;(2)解方程
即可;(2)解方程![]() ,注意分类讨论,以确定
,注意分类讨论,以确定![]() 的符号,从而确定
的符号,从而确定![]() 的单调性,得极大值或极小值(极值点多时,最好列表表示);(3)题意就是方程
的单调性,得极大值或极小值(极值点多时,最好列表表示);(3)题意就是方程![]() 无实数解,即关于
无实数解,即关于![]() 的方程
的方程![]() 在
在![]() 上没有实数解.一般是分类讨论,
上没有实数解.一般是分类讨论,![]() 时,无实数解,
时,无实数解,![]() 时,方程变为
时,方程变为![]() ,因此可通过求函数
,因此可通过求函数![]() 的值域来求得
的值域来求得![]() 的范围.
的范围.
(1)由![]() ,得
,得![]() .
.
又曲线![]() 在点
在点![]() 处的切线平行于
处的切线平行于![]() 轴,
轴,
得![]() ,即
,即![]() ,解得
,解得![]() .
.
(2)![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 为
为![]() 上的增函数,
上的增函数,
所以函数![]() 无极值.
无极值.
②当![]() 时,令
时,令![]() ,得
,得![]() ,
,![]() .
.
![]() ,
,![]() ;
;![]() ,
,![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() 在
在![]() 处取得极小值,且极小值为
处取得极小值,且极小值为![]() ,无极大值.
,无极大值.
综上,当![]() 时,函数
时,函数![]() 无极小值
无极小值
当![]() ,
,![]() 在
在![]() 处取得极小值
处取得极小值![]() ,无极大值.
,无极大值.
(3)当![]() 时,
时,![]()
令![]() ,
,
则直线![]() :
:![]() 与曲线
与曲线![]() 没有公共点,
没有公共点,
等价于方程![]() 在
在![]() 上没有实数解.
上没有实数解.
假设![]() ,此时
,此时![]() ,
,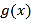 ,
,
又函数![]() 的图象连续不断,由零点存在定理,可知
的图象连续不断,由零点存在定理,可知![]() 在
在![]() 上至少有一解,与“方程
上至少有一解,与“方程![]() 在
在![]() 上没有实数解”矛盾,故
上没有实数解”矛盾,故![]() .
.
又![]() 时,
时,![]() ,知方程
,知方程![]() 在
在![]() 上没有实数解.
上没有实数解.
所以![]() 的最大值为
的最大值为![]() .
.
解法二:
(1)(2)同解法一.
(3)当![]() 时,
时,![]() .
.
直线![]() :
:![]() 与曲线
与曲线![]() 没有公共点,
没有公共点,
等价于关于![]() 的方程
的方程![]() 在
在![]() 上没有实数解,即关于
上没有实数解,即关于![]() 的方程:
的方程:
![]() (*)
(*)
在![]() 上没有实数解.
上没有实数解.
①当![]() 时,方程(*)可化为
时,方程(*)可化为![]() ,在
,在![]() 上没有实数解.
上没有实数解.
②当![]() 时,方程(*)化为
时,方程(*)化为![]() .
.
令![]() ,则有
,则有![]() .
.
令![]() ,得
,得![]() ,
,
当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| 减 |
| 增 |
当![]() 时,
时,![]() ,同时当
,同时当![]() 趋于
趋于![]() 时,
时,![]() 趋于
趋于![]() ,
,
从而![]() 的取值范围为
的取值范围为![]() .
.
所以当![]() 时,方程(*)无实数解, 解得
时,方程(*)无实数解, 解得![]() 的取值范围是
的取值范围是![]() .
.
综上,得![]() 的最大值为
的最大值为![]() .
.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c.已知asin(A+B)=csin![]() .
.
(1)求A;
(2)求sinBsinC的取值范围;
(3)若△ABC的面积为![]() ,周长为8,求a.
,周长为8,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次考试共有12道选择题,每道选择题都有4个不同的选项,其中有且只有一个是正确的,评分标准规定:每题只选一个选项,答对得5分,不答或答错得0分,某考生已确定有8道题的答案是正确的,其余题中,有两道题都可判断两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因为不理解题意只好乱猜,请求出该考生:
(1)得60分的概率;
(2)所得分数![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方体![]() 中,底面ABCD的长AB=4,宽BC=4,高
中,底面ABCD的长AB=4,宽BC=4,高![]() =3,点M,N分别是BC,
=3,点M,N分别是BC,![]() 的中点,点P在上底面
的中点,点P在上底面![]() 中,点Q在
中,点Q在![]() 上,若
上,若![]() ,则PQ长度的最小值是
,则PQ长度的最小值是
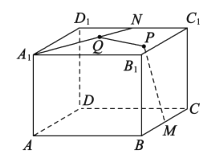
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的右顶点为
的右顶点为![]() ,左焦点为
,左焦点为![]() ,离心率为
,离心率为![]() ,已知
,已知![]() 也是抛物线
也是抛物线![]() 的焦点,
的焦点, ![]() 到准线的距离为
到准线的距离为![]()
(1)求椭圆的方程和抛物线的方程;
(2)过原点的直线交![]() 于
于![]() 两点,点
两点,点![]() 在第一象限,
在第一象限,![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 交
交![]() 于另一点
于另一点![]() .
.
①证明:![]() 三点共线
三点共线
②求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知符号函数sgnx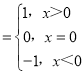 f(x)是定义在R上的减函数,g(x)=f(x)﹣f(ax)(a>1),则( )
f(x)是定义在R上的减函数,g(x)=f(x)﹣f(ax)(a>1),则( )
A.sgn[g(x)]=sgn xB.sgn[g(x)]=﹣sgnx
C.sgn[g(x)]=sgn[f(x)]D.sgn[g(x)]=﹣sgn[f(x)]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了美化校园,要对校园内某一区域作如下设计,如图,已知![]() ,
,![]() ,
,![]() ,在边BC上选一点P. 沿着AP和CP重新栽种花木,图中阴影部分铺上草坪. AP段栽种花木费用是每米3a元,CP段栽种花木费用是每米2a元,其中a是正常数.设
,在边BC上选一点P. 沿着AP和CP重新栽种花木,图中阴影部分铺上草坪. AP段栽种花木费用是每米3a元,CP段栽种花木费用是每米2a元,其中a是正常数.设![]() .
.
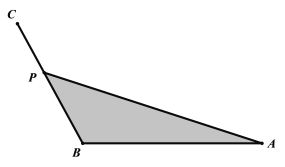
(1)求栽种花木费用y关于θ的函数表达式;
(2)求![]() 的值,使得栽种花木费用y最小.
的值,使得栽种花木费用y最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com