
”¾ĢāÄæ”æŠÄĄķѧ¼Ņ·ÖĪö·¢ĻÖŹÓ¾õŗĶæÕ¼äÄÜĮ¦ÓėŠŌ±šÓŠ¹Ų£¬Ä³ŹżŃ§ŠĖȤŠ”×éĪŖĮĖŃéÖ¤Õāøö½įĀŪ£¬“ÓŠĖȤŠ”×éÖŠ°“·Ö²ć³éŃłµÄ·½·Ø³éČ”50ĆūĶ¬Ń§£ØÄŠ30Å®20£©£¬øųĖłÓŠĶ¬Ń§¼øŗĪĢāŗĶ“śŹżĢāø÷Ņ»Ģā£¬ČĆø÷Ī»Ķ¬Ń§×ŌÓÉŃ”ŌńŅ»µĄĢā½ųŠŠ½ā“š£®Ń”ĢāĒéæöČē±ķ£ŗ£Øµ„Ī»£ŗČĖ£©
¼øŗĪĢā | “śŹżĢā | ×Ü¼Ę | |
ÄŠĶ¬Ń§ | 22 | 8 | 30 |
Å®Ķ¬Ń§ | 8 | 12 | 20 |
×Ü¼Ę | 30 | 20 | 50 |
£Ø1£©ÄÜ·ń¾Ż“ĖÅŠ¶ĻÓŠ97.5%µÄ°ŃĪÕČĻĪŖŹÓ¾õŗĶæÕ¼äÄÜĮ¦ÓėŠŌ±šÓŠ¹Ų£æ
£Ø2£©¾¹ż¶ą“Ī²āŹŌŗ󣬼×Ćæ“Ī½ā“šŅ»µĄ¼øŗĪĢāĖłÓƵď±¼äŌŚ5©7·ÖÖÓ£¬ŅŅĆæ“Ī½ā“šŅ»µĄ¼øŗĪĢāĖłÓƵď±¼äŌŚ6©8·ÖÖÓ£¬ĻÖ¼×”¢ŅŅø÷½āĶ¬Ņ»µĄ¼øŗĪĢā£¬ĒóŅŅ±Č¼×ĻČ½ā“šĶźµÄøÅĀŹ£®
£Ø3£©ĻÖ“ÓŃ”Ōń×ö¼øŗĪĢāµÄ8ĆūÅ®ÉśÖŠČĪŅā³éČ”Į½ČĖ¶ŌĖżĆĒµÄ“šĢāĒéæö½ųŠŠČ«³ĢŃŠ¾æ£¬¼Ē¼×”¢ŅŅĮ½Å®Éś±»³éµ½µÄČĖŹżĪŖX£¬ĒóXµÄ·Ö²¼ĮŠ¼°ŹżŃ§ĘŚĶūE£ØX£©£®
ø½±ķ¼°¹«Ź½£ŗ
P£ØK2”Żk£© | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2= ![]() £®
£®
”¾“š°ø”æ
£Ø1£©½ā£ŗÓɱķÖŠŹż¾ŻµĆK2µÄ¹Ū²āÖµK2= ![]() =
= ![]() £¾5.024£®
£¾5.024£®
ĖłŅŌøł¾ŻĶ³¼ĘÓŠ97.5%µÄ°ŃĪÕČĻĪŖŹÓ¾õŗĶæÕ¼äÄÜĮ¦ÓėŠŌ±šÓŠ¹Ų£®
£Ø2£©½ā£ŗÉč¼×”¢ŅŅ½ā“šŅ»µĄ¼øŗĪĢāµÄŹ±¼ä·Ö±šĪŖx£¬y·ÖÖÓ£¬
Ōņ»ł±¾ŹĀ¼žĀś×ćµÄĒųÓņĪŖ ![]() £ØČēĶ¼ĖłŹ¾£©£®
£ØČēĶ¼ĖłŹ¾£©£®

ÉčŹĀ¼žAĪŖ”°ŅŅ±Č¼×ĻČ×öĶź“ĖµĄĢā”±
ŌņĀś×ćµÄĒųÓņĪŖx£¾y£®
”ąP£ØA£©= ![]() =
= ![]()
¼“ŅŅ±Č¼×ĻČ½ā“šĶźµÄøÅĀŹĪŖ ![]() £®
£®
£Ø3£©½ā£ŗŌŚŃ”Ōń×ö¼øŗĪĢāµÄ8ĆūÅ®ÉśÖŠČĪŅā³éČ”Į½ČĖ£¬³éČ”·½·ØÓŠ ![]() =28 ÖÖ£¬
=28 ÖÖ£¬
ĘäÖŠ¼×”¢ŅŅĮ½ČĖ¶¼²»±»±»³éµ½ÓŠ ![]() =15ÖÖ£»Ē”ÓŠŅ»ČĖ±»³éµ½ÓŠ
=15ÖÖ£»Ē”ÓŠŅ»ČĖ±»³éµ½ÓŠ ![]()
![]() =12ÖÖ£»Į½ČĖ¶¼±»³éµ½ÓŠ
=12ÖÖ£»Į½ČĖ¶¼±»³éµ½ÓŠ ![]() =1ÖÖ£®
=1ÖÖ£®
XæÉÄÜȔֵĪŖ0£¬1£¬2£¬
P£ØX=0£©= ![]() £¬P£ØX=1£©=
£¬P£ØX=1£©= ![]() £¬P£ØX=2£©=
£¬P£ØX=2£©= ![]() £®
£®
XµÄ·Ö²¼ĮŠĪŖ£ŗ
X | 0 | 1 | 2 |
P |
|
|
|
”ąE£ØX£©=0”Į ![]() +1”Į
+1”Į ![]() +2”Į
+2”Į ![]() =
= ![]()
”¾½āĪö”æ£Ø1£©¼ĘĖćK2 £¬ ¶ŌÕÕø½±ķ×ö½įĀŪ£»£Ø2£©×÷³ö¼×£¬ŅŅĮ½ČĖ½ā“šŹ±¼äµÄĘ½ĆęĒųÓņ£¬ÕŅ³öŅŅ±Č¼×Ōē×öĶź¶ŌÓŚµÄĒųÓņ£¬ŌņĒųÓņĆ껿µÄ±ČÖµ¼“ĪŖĖłĒóøÅĀŹ£»£Ø3£©Ź¹ÓĆ×éŗĻŹż¹«Ź½ŗĶ¹ÅµäøÅŠĶµÄøÅĀŹ¼ĘĖć¹«Ź½·Ö±š¼ĘĖćXČ”²»Ķ¬ÖµŹ±µÄøÅĀŹ£¬µĆµ½XµÄ·Ö²¼ĮŠ£¬Ēó³öŹżŃ§ĘŚĶū£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉčµć![]() µÄ×ų±ź·Ö±šĪŖ
µÄ×ų±ź·Ö±šĪŖ![]() £¬Ö±Ļß
£¬Ö±Ļß![]() Ļą½»ÓŚµć
Ļą½»ÓŚµć![]() £¬ĒŅĖüĆĒµÄŠ±ĀŹÖ®»żŹĒ
£¬ĒŅĖüĆĒµÄŠ±ĀŹÖ®»żŹĒ![]() .
.
£Ø1£©Ēóµć![]() µÄ¹ģ¼£
µÄ¹ģ¼£![]() µÄ·½³Ģ£»
µÄ·½³Ģ£»
£Ø2£©Ö±Ļß![]() ÓėĒśĻß
ÓėĒśĻß![]() Ļą½»ÓŚ
Ļą½»ÓŚ![]() Į½µć£¬Čō
Į½µć£¬Čō![]() ŹĒ·ń“ęŌŚŹµŹż
ŹĒ·ń“ęŌŚŹµŹż![]() £¬Ź¹µĆ
£¬Ź¹µĆ![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() ?Čō“ęŌŚ£¬ĒėĒó³ö
?Čō“ęŌŚ£¬ĒėĒó³ö![]() µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ”£
µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĶųøńÖ½ÉĻŠ”Õż·½ŠĪµÄ±ß³¤ĪŖ1£¬“ÖĻß»³öµÄŹĒijøöĖÄĆęĢåµÄČżŹÓĶ¼£¬ŌņøĆĖÄĆęĢåµÄ±ķĆ껿ĪŖ£Ø £© 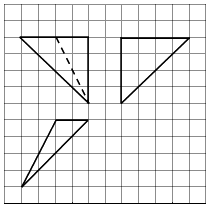
A.8+8 ![]() +4
+4 ![]()
B.8+8 ![]() +2
+2 ![]()
C.2+2 ![]() +
+ ![]()
D.![]() +
+ ![]() +
+ ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijµ„Ī»ĪŖĀĢ»Æ»·¾³£¬ŅĘŌŌĮĖ¼×”¢ŅŅĮ½ÖÖ“óŹ÷ø÷2Öź£®Éč¼×”¢ŅŅĮ½ÖÖ“óŹ÷ŅĘŌŌµÄ³É»īĀŹ·Ö±šĪŖ![]() ŗĶ
ŗĶ![]() £¬ĒŅø÷Öź“óŹ÷ŹĒ·ń³É»ī»„²»Ó°Ļģ£®ĒóŅĘŌŌµÄ4Öź“óŹ÷ÖŠ£ŗ
£¬ĒŅø÷Öź“óŹ÷ŹĒ·ń³É»ī»„²»Ó°Ļģ£®ĒóŅĘŌŌµÄ4Öź“óŹ÷ÖŠ£ŗ
£Ø1£©Į½ÖÖ“óŹ÷ø÷³É»ī1ÖźµÄøÅĀŹ£»
£Ø2£©³É»īµÄÖźŹż![]() µÄ·Ö²¼ĮŠÓėĘŚĶū£®
µÄ·Ö²¼ĮŠÓėĘŚĶū£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() £®
£®
£Ø1£©ĒóĒśĻß![]() ŌŚµć
ŌŚµć![]() “¦µÄĒŠĻß·½³Ģ£»
“¦µÄĒŠĻß·½³Ģ£»
£Ø2£©ĒóŗÆŹż![]() µÄµ„µ÷Ēų¼ä¼°¼«Öµ£»
µÄµ„µ÷Ēų¼ä¼°¼«Öµ£»
£Ø3£©¶Ō![]() £¬
£¬ ![]() ³ÉĮ¢£¬Ē󏵏ż
³ÉĮ¢£¬Ē󏵏ż![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŹżĮŠ{an}ÖŠ£¬a1=1£¬an £¬ an+1ŹĒ·½³Ģx2©£Ø2n+1£©x+ ![]() µÄĮ½øöøł£¬ŌņŹżĮŠ{bn}µÄĒ°nĻīŗĶSn=£Ø £©
µÄĮ½øöøł£¬ŌņŹżĮŠ{bn}µÄĒ°nĻīŗĶSn=£Ø £©
A.![]()
B.![]()
C.![]()
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() £¬
£¬ ![]() £ØĘäÖŠ
£ØĘäÖŠ![]() £¬
£¬ ![]() £©£¬ĒŅŗÆŹż
£©£¬ĒŅŗÆŹż![]() µÄĶ¼ĻóŌŚµć
µÄĶ¼ĻóŌŚµć![]() “¦µÄĒŠĻßÓėŗÆŹż
“¦µÄĒŠĻßÓėŗÆŹż![]() µÄĶ¼ĻóŌŚµć
µÄĶ¼ĻóŌŚµć![]() “¦µÄĒŠĻßÖŲŗĻ£®
“¦µÄĒŠĻßÖŲŗĻ£®
£Ø1£©Ē󏵏ż![]() £¬
£¬ ![]() µÄÖµ£»
掙术
£Ø2£©¼ĒŗÆŹż![]() £¬ŹĒ·ń“ęŌŚ×īŠ”µÄÕż³£Źż
£¬ŹĒ·ń“ęŌŚ×īŠ”µÄÕż³£Źż![]() £¬Ź¹µĆµ±
£¬Ź¹µĆµ±![]() Ź±£¬¶ŌÓŚČĪŅāÕżŹµŹż
Ź±£¬¶ŌÓŚČĪŅāÕżŹµŹż![]() £¬²»µČŹ½
£¬²»µČŹ½![]() ŗć³ÉĮ¢£æøų³öÄćµÄ½įĀŪ£¬²¢ĖµĆ÷½įĀŪµÄŗĻĄķŠŌ£®
ŗć³ÉĮ¢£æøų³öÄćµÄ½įĀŪ£¬²¢ĖµĆ÷½įĀŪµÄŗĻĄķŠŌ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æµ± ![]() Ź±£¬²»µČŹ½
Ź±£¬²»µČŹ½ ![]() ŗć³ÉĮ¢£¬ŌņŹµŹżaµÄȔֵ·¶Ī§ŹĒ£Ø £©
ŗć³ÉĮ¢£¬ŌņŹµŹżaµÄȔֵ·¶Ī§ŹĒ£Ø £©
A.[-5,-3]
B.[-6,1]
C.[-6,-2]
D.[-4,-3]
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com